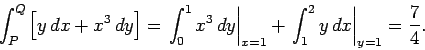integrali di linea
In matematica, un integrale di linea o integrale curvilineo è un integrale in cui la funzione da integrare è valutata lungo un cammino o una curva. Per essere meno astratti, pensiamo all'applicazione degli integrali di linea alla fisica. Consideriamo una forza F il cui valore dipende dalla sua posizione in uno spazio bidimensionale, F(x, y), evidentemente il lavoro compito da questa forza per spostare un oggetto di massa, m, dal punto P al punto Q, dipenderà dal percorso effettuato (perché F varia a seconda del percorso).
Per esempio, consideriamo l'integrale di
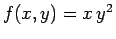 tra
tra 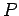 e
e 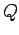 lungo i due differenti percorsi indicati in figura 1.
lungo i due differenti percorsi indicati in figura 1.
Figura 1:
un esempio di integrale di linea
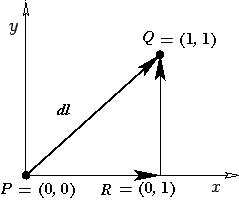 |
dove 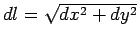 .
.
Lungo il percorso PQ abbiamo 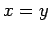 , per cui
, per cui
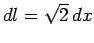 . così
. così
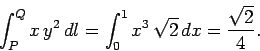 |
(1326) |
L'integrazione lungo il percorso PR-RQ fornisce
Si noti che l'integrale dipende dal percorso seguito per passare dal punto iniziale a quello finale.
Il tipo più comune di integrale di linea è quello in cui i contributi da 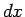 e
e 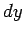 sono valutati separatamente, piuttosto che attraverso la lunghezza del percorso
sono valutati separatamente, piuttosto che attraverso la lunghezza del percorso 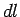 : per es.,
: per es.,
![\begin{displaymath}
\int_P^Q \left[ f(x,y)\,dx + g(x,y)\,dy\right].
\end{displaymath}](integralelinea_files/img3385.png) |
(1328) |
Come esempio di questa notazione, consideriamo l'integrale
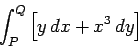 |
(1329) |
da calcolare lungo i due percorsi indicati in figura 2.
Figura 2:
un esempio di integrale di linea
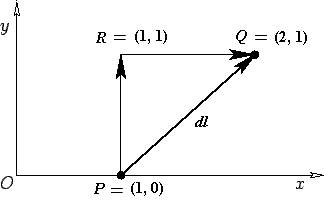 |
Lungo il percorso PQ abbiamo 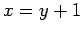 e
e 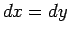 , quindi
, quindi
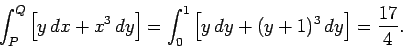 |
(1330) |
Lungo il percorso PR-RQ (si tenga conto che dx = dy)
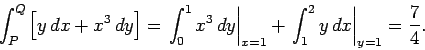 |
(1331) |
Anche questa volta l'integrale dipende dal percorso d'integrazione.
Supponiamo di trovare un integrale di linea che non dipende dal percorso d'integrazione. Ne segue che
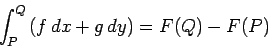 |
(1332) |
per alcune funzioni 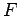 . Dato
. Dato 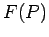 per un punto
per un punto 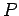 nel
nel 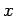 -
-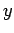 piano, allora
piano, allora
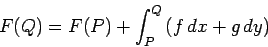 |
(1333) |
definisce 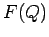 per tutti gli altri punti nel piano. Noi possiamo tracciare una mappa del contorno del
per tutti gli altri punti nel piano. Noi possiamo tracciare una mappa del contorno del 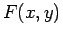 .
L'integrale di linea tra i punti
.
L'integrale di linea tra i punti 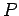 and
and  è semplicemente la variazione in altezza nel profilo (contour) della mappa tra questi due punti:
è semplicemente la variazione in altezza nel profilo (contour) della mappa tra questi due punti:
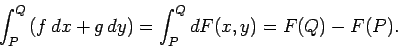 |
(1334) |
Così,
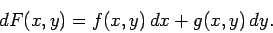 |
(1335) |
Per esempio, se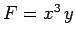 allora
allora
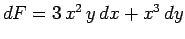 e
e
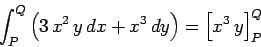 |
(1336) |
è indipendente dal percorso d'integrazione.
E' chiaro che vi sono due tipi distinti di integrali di linea. Quelli che dipendono solo dai loro punti estremi e non dal percorso d'integrazione, e quelli che sipendono sia dai punti estremi che dal percorso d'integrazione.
tredotto da: http: //farside.ph.utexas.edu/teaching/
differenziali esatti
 1 1 |
 2 2 |
 3 3 |
 4 4 |
 5 5 |
6 |
 7 7 |
 8 8 |
 HOME PAGE HOME PAGE |


![]() tra
tra ![]() e
e ![]() lungo i due differenti percorsi indicati in figura 1.
lungo i due differenti percorsi indicati in figura 1.
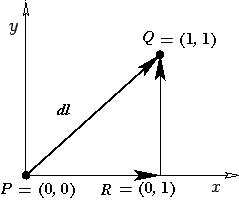
![]() .
.
![]() , per cui
, per cui
![]() . così
. così
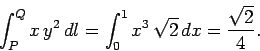
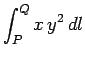
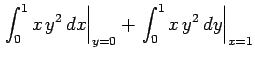
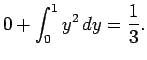
![]() e
e ![]() sono valutati separatamente, piuttosto che attraverso la lunghezza del percorso
sono valutati separatamente, piuttosto che attraverso la lunghezza del percorso ![]() : per es.,
: per es.,
![]() e
e ![]() , quindi
, quindi