Non è che i ponti sarebbero più sicuri se fosse permesso di progettarli
solo a chi conosce la definizione corretta di un numero reale.3
Se il matematico deve necessariamente seguire un rigore formale in quanto esso è l'unica garanzia della correttezza delle sue inferenze, i fisici e gli ingegneri possono usare il "procedimento del boscaiolo" in quanto: 1) non devono dimostrare tesi matematiche; 2) il rigore formale è sostituito dalla verifica sperimentale dei modelli matematici utilizzati.
 Moltissime teorizzazioni della matematica NON sono state ottenute dai matematici carpendole dall'albero della conoscenza, ma sono state prima abbozzate da persone spinte dalla necessità di risolvere problemi pratici, e poi riviste e approfondite in modo formale. Dunque, se questo è il naturale processo della mente umana, non si capisce per quale ragione nell'insegnare la matematica si debba percorrere il cammino inverso, come se la teoria fosse nata per prima. Come introduzione è preferibile sviluppare un percorso didattico che per quanto possibile ricostruisca proprio la genesi storica degli strumenti matematici.
Moltissime teorizzazioni della matematica NON sono state ottenute dai matematici carpendole dall'albero della conoscenza, ma sono state prima abbozzate da persone spinte dalla necessità di risolvere problemi pratici, e poi riviste e approfondite in modo formale. Dunque, se questo è il naturale processo della mente umana, non si capisce per quale ragione nell'insegnare la matematica si debba percorrere il cammino inverso, come se la teoria fosse nata per prima. Come introduzione è preferibile sviluppare un percorso didattico che per quanto possibile ricostruisca proprio la genesi storica degli strumenti matematici.
Credo di aver dato spazio sufficiente a questa premessa, che è anche una giustificazione - resa accettabile dal fatto che questa sintesi ha valore unicamente propedeutico per seguire le questioni che vedono l'analisi necessaria allo studio elementare di fenomeni fisici e chimici - e quindi passiamo subito alla nostra discussione.
la matematica dei greci
La cosiddetta matematica dei greci, è convenzionalmente distinta in due periodi. Nel primo periodo, quello della massima importanza economica e politica delle città greche e delle loro colonie, si colloca la matematica sviluppata dai matematici di queste città. Nel successivo periodo ellenistico (che si può far iniziare nel 323 a.C. e concludere intorno al V secolo dopo Cristo) si colloca la produzione di tutti gli autori che operarono nel mondo ellenistico accomunati dell'uso della lingua greca. Molte delle più grandi menti di questo periodo come Archimede e Apollonio non vissero nell'area geografica corrispondente all'attuale Grecia, pur essendo protagonisti della cultura ellenistica di lingua greca diffusasi in molte aree mediterranee.
I più antichi testi di matematica trovati in greco sono stati scritti posteriormente al periodo ellenistico; tuttavia, parecchi di essi sono ritenuti copie di opere scritte durante e anche prima di questo periodo. D'altra parte, la datazione della matematica greca è più attendibile rispetto a quella degli scritti matematici più antichi, poiché esistono numerose cronologie che, sovrapponendosi, riportano gli avvenimenti anno per anno fino ad oggi.
La matematica greca è molto più moderna di quella sviluppata dalle precedenti culture quali quella egiziana e babilonese, in quanto queste ultime utilizzavano il ragionamento empirico, cioè induttivo, che sfruttava le osservazioni ripetute per fondare le regole della matematica. La matematica greca, invece, è fondata sul ragionamento deduttivo, che partendo da assiomi più o meno ovvi usa rigorosi ragionamenti per dimostrare teoremi; su questa idea ancor oggi si basa tutta la matematica moderna. I Greci si occuparono quasi esclusivamente di geometria e, secondo i loro canoni si potevano usare solo due strumenti per la costruzione e lo studio di figure geometriche: la riga (non taccata) e il compasso (che si chiudeva non appena sollevato dal foglio, e quindi non poteva servire per riportare una misura). Ragionamenti che coinvolgevano altri strumenti erano a volte utilizzati, ma venivano considerati non rigorosi.
Si ritiene che la matematica greca abbia avuto inizio con Talete di Mileto (624-546 a.C. ca.) e Pitagora di Samo (582 — 507 a.C. ca.). Sebbene sia un argomento di dibattito, qualche influenza derivò dalle idee della matematica egiziana, babilonese e indiana.
Talete si occupò di geometria, scoprendo per esempio il teorema secondo il quale un triangolo inscritto in una semicirconferenza è sempre rettangolo e molte proposizioni riguardanti i triangoli simili. Grazie a tali teoremi, secondo la tradizione riuscì a determinare l'altezza della piramide di Cheope, misurando la sua ombra.
Pitagora, invece, fu il fondatore della Scuola Pitagorica, la quale però era quella che oggi - con una connotazione riduttivamente negativa - definiremmo una setta i cui membri si dedicavano ad una ricerca mistico-filosofica che coincideva con la matematica. Tutta la filosofia della setta era fondata sui numeri naturali e sui loro quozienti, i numeri razionali.
Gli adepti della setta dovevano rigidamente attenersi a regole precise che regolavano la vita pubblica e privata: rispettare gli dei, fare ogni sera un esame di coscienza e ogni mattina un programma per il giorno che iniziava; non cibarsi di carne (perché credevano alla metempsicosi) e di fave (ritenute il mezzo più adatto per permettere ai morti di comunicare con il mondo dei vivi), non spezzare il pane o attizzare il fuoco con metallo, non indossare panni di lana o anelli, non raccogliere ciò che era caduto. Occorreva rispettare la regola del silenzio, praticare la comunione dei beni e non si era mai ammessi alla presenza del maestro (Pitagora), che parlava ai novizi (detti acusmatici) i quali potevano solo ascoltare il maestro celato da una tenda. L'insegnamento di Pitagora veniva appreso come una rivelazione divina, in forma dogmatica, come attesta la formula rituale in uso nella setta "autòs èphe": "lo ha detto lui". Gli insegnamenti venivano tramandati oralmente e su di essi si doveva mantenere il segreto. La divulgazione dei segreti al di fuori della cerchia degli iniziati poteva costare anche la morte.
I pitagorici avevano una visione "matematica" del mondo, una prospettiva in cui tutto doveva essere ricondotto al numero. Nell'ambito delle ricerche matematiche da loro effettuate, i loro studi sui numeri pari e dispari, sui numeri primi e sugli irrazionali furono fondamentali per la teoria dei numeri.
Per i pitagorici "arché" è numero; una delle massime pitagoriche recitava: "che cosa c'è di più saggio? il numero. Che cosa c’è di più bello? l'armonia". Essi non consideravano i numeri come entità astratte, bensì concrete, ossia come grandezze spaziali, aventi estensione e forma, rappresentate geometricamente mediante configurazioni di punti. L'unità veniva designata come un punto, i numeri successivi attraverso figure geometriche costruite da insiemi di punti e indicate attraverso l'uso di sassolini. I numeri sono dunque, per i pitagorici, cose reali. Per questo, la scuola pitagorica individuò nei numeri e nelle loro proprietà, piuttosto che nell'acqua e nell'aria, gli elementi fondamentali di cui cose sono costituite.
Non ci è pervenuta nessuna opera classica relativa all'arte del calcolo dei Greci, ma dai matematici bizantini del Medioevo si sa che usavano tabelle di prodotti forse simili a quelle dei Babilonesi, mentre per eseguire calcoli con frazioni usavano scomporle in unità frazionarie, come gli Egizi. I Greci, per i loro calcoli utilizzavano l'abaco, costituito da una tavoletta di legno con scanalature parallele nelle quali erano posti dei sassolini (in latino calculi, da cui la parola calcolo) che, spostati in maniera opportuna, permettevano di eseguire le più importanti operazioni aritmetiche: una sorta di pallottoliere.
Inizialmente, i matematici pitagorici avevano concepito la linea come una successione finita di punti di dimensioni finite. Tale concezione, per così dire "granulare" della linea, presentava il vantaggio di consentire uno stretto collegamento fra geometria ed aritmetica. In pratica, per conoscere la misura della lunghezza di una determinata linea è sufficiente contare i punti che la costituiscono. Se raddoppiamo la lunghezza della linea, basterà raddoppiare il numero dei punti; se la triplichiamo, basterà triplicarlo; e così via. Alla base di questa concezione vi è l'idea del punto come elemento matematico corrispondente all'unità e perciò, in qualche modo, esteso e occupante una data posizione nello spazio.
il teorema di Pitagora e i numeri irrazionali
I pitagorici diedero importanti contributi alla geometria, primo fra tutti la dimostrazione del Teorema di Pitagora (in realtà, la prima testimonianza nota relativa al teorema di Pitagora è contenuta in una tavoletta paleobabilonese, databile tra il 1800 e il 1600 a. C., in cui è disegnato un quadrato con le due diagonali). La scoperta del Teorema mostrò l'esistenza dei numeri irrazionali, ossia quei numeri che non si possono scrivere come rapporto di numeri naturali (come per esempio il numero pi greco o la radice del numero 2) e fu sconvolgente. I pitagorici si accorsero infatti che non esiste un segmento che, se assunto come unità, misuri con numeri interi sia il lato di un quadrato che la sua diagonale; questo risultato prese il nome di incommensurabilità della diagonale del quadrato. Per le loro convinzioni decisero di non divulgare questa notizia all'esterno della scuola.
Non c'è da meravigliarsi della proibizione imposta ai membri della setta di rivelare ad altri queste scoperte considerate blasfeme; tuttavia, secondo una delle ipotesi più diffuse, uno dei discepoli, Ippaso da Metaponto divulgò il segreto. Per il suo tradimento, Ippaso venne messo al bando con ignominia dalla scuola dei pitagorici che, si racconta, gli innalzarono un monumento funebre, perché fosse chiaro che per loro era morto. La sua "morte" non impedì che lo scandalo si diffondesse rapidamente tra i cultori della matematica e finisse per scuotere dalle fondamenta l'intera concezione pitagorica.
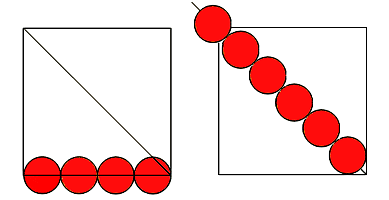 |
| calibrando opportunamente delle sferette, queste trovano posto lungo un lato di un quadrato, ma sferette delle stesse dimensioni non coprono in numero intero la diagonale del quadrato. |
I pitagorici, come conseguenza della loro scoperta, dovettero ammettere che un segmento e in generale una figura geometrica era costituita da infiniti punti di dimensione nulla, contrariamente a quanto ritenevano, cioè che i punti avessero una dimensione, fossero molto piccoli e tutti uguali, ma non nulli.
La scoperta dell'incommensurabilità del lato di un quadrato e della sua diagonale era destinata a rivoluzionare tutto il pensiero geometrico, a partire dal concetto di punto: evidentemente, non poteva più essere concepito come punto-monade occupante una porzione di spazio, bensì unicamente come punto ideale, avente una posizione, però assolutamente privo di dimensioni.
E' proprio l'incommensurabiltà fra il lato di un quadrato e al sua diagonale a richiedere che un segmento sia costituito da un numero infinito di punti. I greci pensarono di riuscire a superare queste difficoltà passando ad un ragionamento geometrico indipendente dall'aritmetica e "interpretando la geometria come studio del continuo e l'aritmetica come studio del discontinuo".
L'esistenza dei numeri irrazionali creò lo scollamento tra la teoria e la realtà. Se i punti che costituivano un segmento di linea erano infiniti, si creava un paradosso: come è possibile che una serie di numeri infinita dia origine ad una somma finita, ovverosia la lunghezza del segmento?
La questione sembra facile... per esempio, consideriamo la successione ottenuta dividendo una bacchetta di legno in due parti; di queste due parti una metà la tagliamo ulteriormente in due parti; di queste altre due parti una metà la tagliamo ulteriormente in due parti; ecc. In numeri, otteniamo:
1/2 + 1/4 + 1/8 + 1/16 + ... + 1/2n = 1
E' ovvio che la somma sia unitaria, perché riunendo i pezzi della bacchetta, la ricomponiamo e certo la sua lunghezza è certamente finita; tuttavia, l'intuito, secondo il quale da una bacchetta, per quanto e per come la si tagli, si otterranno comunque dei pezzi che uniti saranno della lunghezza dela bacchetta non è un buon maestro... infatti, se consideriamo la serie:
1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + ... + 1/n = la serie (ovverosia la somma dei numeri) è divergente!
questa serie, nota come armonica, che contiene numeri razionali (alcuni con una parte periodica che si ripete all'infinito) fu scoperta dai pitagorici nel 500 a.C.; ma la dimostrazione più antica della sua divergenza è dovuta a Nicola Oresme (ca. 1323–1382).
E' ovvio che qualcosa non andava: come può uno spazio infinitamente divisibile essere finito o non finito a seconda di come lo si divide? La pratica è una cosa, la teoria è un'altra?
i problemi dell'infinito
La somma di due o più numeri costituisce un'operazione ben definita, che si impara fin dalle scuole elementari; però, sommare infiniti numeri è un'operazione che per avere un senso richiede una definizione molto più complessa (nel nostro esempio questa complessità è celata dall'uso di numeri particolarmente semplici).
Quella di somma infinita (che nel linguaggio matematico odierno è detta serie) è un'operazione per la quale una definizione di un certo rigore apparirà solo verso il 1700 (e quella attualmente in uso solo nell'800), quindi ben più di 2000 anni dopo che Zenone ebbe segnalato con il suo paradosso la difficoltà di questo concetto.
Per evidenziare quanto sia problematico definire il concetto di somma infinita, consideriamo la seguente somma (infinita):
1 - 1 + 1 - 1 + 1 - 1 + 1- ...
Il matematico Guido Grandi (1671-1742), professore all'università di Pisa, ne ricavò il seguente paradosso, ottenuto raggruppando gli addendi in due modi differenti, eppure entrambi ragionevoli:
1 + (-1 + 1) + (-1 + 1) + ... = 1
(1 - 1) + (1 - 1) + (1 - 1) + ... = 0
Quindi il risultato della somma è sia 0 che 1 .
Questa osservazione comporta che quando si cerca di estendere alle quantità infinite il nostro modo usuale di operare con le quantità finite è necessario definire nuove regole e procedimenti, se non si vuole cadere in contraddizioni o formule prive di senso.
Le considerazioni precedenti ci indicano che Zenone con il suo paradosso (e con gli altri di cui parleremo più avanti) aveva "messo il dito nella piaga": aveva segnalato la difficoltà di essere rigorosi nei ragionamenti riguardanti l'infinito, mostrando come anche nozioni di uso comune (principalmente quelle riguardanti il movimento) potessero, quando analizzate da vicino, racchiudere una grande complessità e come la loro matematizzazione fosse un'opera molto ardua.
l'hotel infinito e il paradosso di Zenone
Quando gli elementi che formano un insieme sono in numero naturale non precisabile, l'insieme si dice infinito. Gli insiemi infiniti possono dare origine a paradossi quali quello dell'"Hotel infinito" formulato per la prima volta da David Hilbert nel 1920.
Immaginiamo che in qualche punto della galassia ci sia un hotel con un numero infinito di stanze, ciascuna delle quali sia occupata. Supponiamo si presenti un'astronauta a chiedere una camera e il proprietario risponda:
"Beh, saremmo al completo, ma posso sicuramente trovarle una sistemazione".
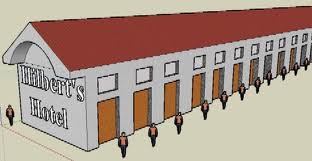 L'albergatore sposterà tutti i clienti nella camera successiva (l'ospite della 1 alla 2, quello della 2 alla 3, etc.); in questo modo, benché l'albergo sia pieno è comunque, essendo infinito, possibile sistemare il nuovo ospite.
Immaginiamo ancòra che successivamente arrivi un'astronave con un numero infinito di nuovi ospiti.
L'albergatore sposterà tutti i clienti nella camera successiva (l'ospite della 1 alla 2, quello della 2 alla 3, etc.); in questo modo, benché l'albergo sia pieno è comunque, essendo infinito, possibile sistemare il nuovo ospite.
Immaginiamo ancòra che successivamente arrivi un'astronave con un numero infinito di nuovi ospiti.
In questo caso, l'albergatore prima che l'astronave "attracchi", potrebbe chiedere a tutti gli ospiti dell'albergo di spostarsi nel modo visto in precedenza, però questa volta decide di spostare ogni ospite nella stanza con numero doppio rispetto a quello attuale (dalla 1 alla 2, dalla 2 alla 4,etc.). In questo modo vengono liberate tutte le camere con i numeri dispari, che sono essi stessi infiniti!
La scoperta dei numeri irrazionali, influenzò certamente il pensiero filosofico. A questo proposito, di tutti i paradossi noti, quelli di Hilbert e di Zenone sono sicuramente i più noti, perché sono molto semplici nella loro formulazione e d'acchito sono assurdi. I paradossi di Zenone, però furono i primi che avevano a che fare con i numeri irrazionali. Per esempio, notissimo è il paradosso di Achille e la tartaruga: entrambi decidono di gareggiare l'uno contro l'altra in una corsa. Achille, per avvantaggiare la tartaruga, evidentemente più lenta, le concede un certo vantaggio. Sappiamo che Achille ad ogni passo dimezza la distanza che lo separa dalla tartaruga e tuttavia non riuscirà a raggiungerla. Questo perché, secondo Zenone, e contrariamente alla realtà, anche dimezzando di volta in volta la distanza, questa sarà sempre piccolissima, ma... mai nulla.
Questo paradosso è simile all'altrettanto famoso paradosso della freccia, sempre di Zenone, che, scagliata contro il suo bersaglio, non lo raggiungerà mai per lo stesso motivo.

Il problema appariva di impossibile soluzione per due ragioni:
- era impensabile che una somma infinita di termini potesse dare come risultato un numero finito.
- In quei tempi le operazioni aritmetiche di base costituivano attività molto complesse ed impegnative; è stato il metodo noto come il "Metodo degli indiani" (in latino Modus Indorum), che ha condotto all'aritmetica che conosciamo oggi. L'aritmetica indiana è stata molto più semplice di quella greca, a causa della semplicità del sistema di numerazione indiano, che per primo è riuscito a servirsi del numero zero e di una notazione posizionale. Però, bisognava aspettare ancòra molto, molto tempo!
Il primo problema venne risolto da Archimede, il quale dimostrò che la serie seguente convergeva:
1 + 1/4 + 1/16 + 1/32 + 1/64 + 1/256 + ... = 4/3
in qualche modo il paradosso di Zenone poteva già trovare una soluzione o quantomeno diventava meno ostico. Ma trovò finalmente soluzione solo grazie al calcolo infitesimale sviluppato da Newton e Leibniz. Con gli strumenti da loro fornitici, è stato possibile dimostrare che la somma di infiniti numeri positivi, purché soddisfino a determinate condizioni, dà come risultato un numero finito.
soluzione del paradosso di Zenone
 Il problema è formulato in questo modo: Achille si muove con velocità V, la tartaruga con velocità v, tali che V > v. La tartaruga parte rispetto ad Achille con un vantaggio che possiamo quantificare con una distanza, d. Il tempo che Achille impiegherà a raggiungere la posizione di partenza della tartaruga sarà dato da:
Il problema è formulato in questo modo: Achille si muove con velocità V, la tartaruga con velocità v, tali che V > v. La tartaruga parte rispetto ad Achille con un vantaggio che possiamo quantificare con una distanza, d. Il tempo che Achille impiegherà a raggiungere la posizione di partenza della tartaruga sarà dato da:
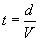
durante questo tempo, la tartaruga avrà percorso lo spazio x1
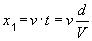
Achille percorrerà questo spazio ulteriore nel tempo t1
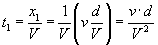
nel frattempo, la tartaruga avrà percorso un secondo tratto x2
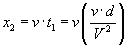
Achille percorrerà questo spazio ulteriore nel tempo t2
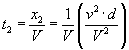
ripetendo il rgionamento, troviamo il termine generale della serie:
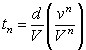
la serie di cui sopra si dimostra che è convergente e la somma è pari a:
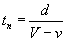
E' facile vedere che se Achille percorre 2 m/sec (con l'armatura e lo scudo è ragionevole), la tartaruga 0,01 m/sec; d = 100 m. Allora Achille raggiungerà la tartaruga (che Zenone lo credesse o no) dopo meno di 50,3 sec.
Il paradosso di Zenone raccontato con i passi che vanno a rimpicciolirsi può però essere un ottimo modo per introdurre gli infinitesimi e il calcolo infinitesimale. La soluzione matematica - trovata dopo cira duemila anni - fa sparire il paradosso (almeno in termini matematici), che però non poteva essere risolto con gli strumenti matematici dei greci.
i problemi delle serie infinite
Non vi è alcun senso fisico nella continuità dello spazio, che anzi a piccole scale è smentita dall'osservazione. Il sistema dei numeri reali è, di per sé, una struttura dotata di certe proprietà, in parte assiomatiche e in parte di comodo, formulata - come abbiamo accennato - in un lungo arco temporale e costata molta fatica. Occorre però molta cautela nell'attribuire al mondo fisico le stesse proprietà del sistema dei numeri reali per semplice trasporto di struttura.
Le serie, così come gli integrali e il concetto di limite hanno una propria effettiva coerenza. I paradossi nascono nel momento in cui notiamo che la realtà non aderisce perfettamente al modello, ma questo è in fin dei conti un falso problema, dato che l'insieme dei numeri reali e il mondo che vogliamo esprimere con questo sistema numerico-topologico-geometrico sono entità nettamente separate (e delle due conosciamo realmente solo la prima, in quanto è una costruzione della mente umana).
Ecco alcuni elementi della costruzione matematica che devono essere tenuti a mente:
- una somma di infiniti termini non nulli può dare un valore finito;
- una somma di aree di rettangoli di base infinitesima può dare un'area finita;
- un numero infinito di elementi può concentrarsi attorno ad un punto fissato dello spazio, spazio che è tale per cui, presi ad arbitrio due punti distinti comunque piccoli, tra essi ne esiste un terzo;
- una retta (infinita) può trovare per ogni suo punto una corrispondenza con i punti su un segmento (finito).
Tutte queste proprietà hanno una propria coerenza strutturale; se poi il mondo non funziona così (fino a prova contraria la materia, arrivati a scale quantistiche, non è divisibile in nessun senso ragionevole, né ha senso fisico pensare a scale di lunghezza che siano inferiori alla minima dimensione misurabile sperimentalmente) il discorso è un altro: pazienza, non abbiamo di meglio. I paradossi di Hilbert e di Zenone sono un non-sense in quanto combinano la realtà fisica con quella matematica: lo spazio matematico non è quantizzato, mentre lo è quello fisico. Così, noi risolviamo un problema fisico con strumenti pensati per un problema matematico. Forse non è corretto. Forse la tecnica del boscaiolo può andar bene, però stiamo lasciando la coerenza e la certezza di un sistema deduttivo, con un salto induttivo nel sistema reale...
definizione di limite di una funzione
Una frase come "Vediamo subito che..." è fin troppo ben nota tra i matematici,
come le sue compagne in infamia "È ovvio che..." ed "Ora, chiaramente, ...";
vogliono dire che il lettore si deve aspettare ore o giorni di fatica da spaccarsi
la testa per illuminare l'oscurità - e scoprire magari alla fine che chi le ha scritte
non si ricorda nemmeno più perché fosse ovvio.4
Ora che ci siamo fatti un'idea seppur rozza dei concetti di infinito e infinitesimo, esaminiamone un'applicazione al calcolo dei limiti.
Per introdurre il concetto di limite, prendiamo le mosse da un esempio pratico: consideriamo la funzione y = x2 -1/ (x + 1) definita in R ; essa evidentemente non è definita nel punto x = -1 (porge la forma 0/0)
Ora, rielaboriamo la stessa funzione y* = (x + 1)(x - 1)/(x + 1) = x -1
La funzione y evidentemente differisce dalla y* in quanto sebbene quest'ultima è definita per qualsiasi valore di x, è ottenuta per semplificazione della precedente (ricordiamoci che la semplificazione è valida solo per x diverso da 1), e dunque le due funzioni y e y* pur assumendo gli stessi valori (eccetto per il valore di x = -1) , non sono uguali.
Il problema, però è cercare di capire quanto queste due funzioni sono differenti. Evidentemente lo sono per x = -1 in quanto mentre y non è definita, y*(-1) = -2
Però, se invece di x = -1 consideriamo x = -0,1 o meglio x = -0,01 e perché no x = -0,0000001 e così via, superiamo il punto di singolarità della funzione y e possiamo stipulare una identificazione escluso il punto x = -1 tra le due funzioni.
Vediamo di esprimere in modo più formale queste considerazioni.
Sia y = f(x) una funzione definita in un insieme E e sia x0 un punto di accumulazione per E (vedremo che x0 può anche non appartenere ad E).
Definizione: la funzione f(x) si dice convergente nel punto x0 su E se esiste un numero reale l ("elle") che gode della seguente proprietà: scelto un qualsiasi numero reale piccolo quanto si voglia ε> 0, si può sempre trovare in corrispondenza un intorno I di x0 dipendente da ε < tale che, per tutti gli x di E diversi da x0 e contenuti nell'intorno I, risulti:
l - ε < f(x) < l - ε oppure, in valore assoluto: | f(x) - l |< ε
Ciò si esprime simbolicamente scrivendo:
Questo simbolismo, tradotto in pratica, significa che percorrendo la funzione, avvicinandosi ad x0 lungo le ascisse, ci avviciniamo anche al valore l lungo le ordinate.
Proviamo a verificare se effettivamente -2 è il limite della funzione y:
dobbiamo applicare la definizione di limite in cui f(x) = x2 -1/ (x + 1) e l = -2
pertanto dobbiamo verificare la disequazione: | x2 -1/ (x + 1) - l |< ε
risolvere questa disequazione, per x ≠ -1 equivale a risolvere la y*:
| (x - 1) + 2 |< ε
cioé il sistema:
-1 - ε < x < -1 + ε
ed effettivamente qualunque valore positivo e piccolo a piacere attribuiamo a ε, si ottiene un intorno completo del punto x = -1 e le disequazioni sono soddisfatte.
Notiamo esplicitamente che la funzione y non è definita nel punto x = -1 (ecco perché il punto x0 non appartiene a E) ma esiste il limite per x → -1 e questo limite vale 0
Tutta questa discussione si riassume sinteticamente con questo simbolismo:
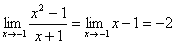
e si legge: il limite della funzione y per x tendente a -1 è -2
Per curiosità, il lettore può verificare che x = 2 non è il limite della funzione. Infatti: | (x - 1) -2| < ε e quindi 3 - ε < x < 3 + ε , che non è un intorno di -1.

Non è negli scopi di questa introduzione fornire altri esempi a proposito di calcolo dei limiti; quello che importa sottolineare è che data una funzione y = f(x) non definita nel punto x0 , con l'operazione di passaggio al limite calcoliamo il valore che assumerebbe la funzione in questione se ci avvicinassimo sempre più al punto singolare e tuttavia senza raggiungerlo mai.
la natura non è markoviana
la natura non è sinonimo di continuità, siamo noi che cerchiamo di regolarizzare i fenomeni con le nostre equazioni differenziali.
Una catena, o meglio concatenazione, di Markov esprime il concetto di una sequenza di eventi dipendenti l'uno dall'altro. Così, una sequenza x1, x2, ..., xn, è markoviana se il fatto di conoscere xn-1, ci permette di calcolare xn.
Per esempio, il notissimo gioco dell'oca ha la caratteristica di essere markoviano. Ciò vuol dire che il futuro del giocatore dipende da dove si trova ora e non dal passato, cioè da come ci è arrivato ("dimmi dove sei e ti dirò dove andrai"). Infatti il numero di caselle in cui l'oca si dovrà spostare dipende dal lancio di un dado: il numero che esce di volta in volta non dipende dal lancio precedente.
 In una sequenza markoviana, i cambiamenti di un sistema tra il tempo t e il tempo t +1 dipendono unicamente dallo stato nel tempo t. Però in natura, questi cambiamenti possono dipendere dallo stato del sistema in t -1. Per esempio, il tempo di domani dipende da quello di oggi, che a sua volta dipende da quello di ieri. Certo, detta così sembra contraddire quello che abbiamo detto a proposto del gioco dell'oca. Però, la cosa è chiara se pensiamo che certi fattori esercitano la loro azione con molto ritardo, per es. i cambiamenti meteorologici.
In una sequenza markoviana, i cambiamenti di un sistema tra il tempo t e il tempo t +1 dipendono unicamente dallo stato nel tempo t. Però in natura, questi cambiamenti possono dipendere dallo stato del sistema in t -1. Per esempio, il tempo di domani dipende da quello di oggi, che a sua volta dipende da quello di ieri. Certo, detta così sembra contraddire quello che abbiamo detto a proposto del gioco dell'oca. Però, la cosa è chiara se pensiamo che certi fattori esercitano la loro azione con molto ritardo, per es. i cambiamenti meteorologici.
Facciamo un esempio chiarificatore: una sfera molto pesante rotola con moto rettilineo uniforme su un asse di legno indeformabile, sicché data la posizione, s, della sfera ad un istante, t, la sua posizione ad un istante successivo, t +1 dipende unicamente da quello attuale. Però se l'asse di legno è deformabile, e la deformazione si propaga con velocità maggiore di quella della sfera, lo stato al tempo t + 1 dipende non solo dallo stato al tempo t, ma anche da quello al tempo t - 1.
Possiamo rendere meno astratto questo esempio, pensando agli effetti della soppressione dei predatori in un parco popolato da lepri: la loro popolazione al tempo (t +1) per un pò dipende da quello al tempo t, ma quando gli effetti della mancanza di predatori iniziano ad essere evidenti, la popolazione delle lepri aumenterà (per effetto di un'azione passata) e questa depaupererà il sottobosco con cui si alimenta...

La principale argomentazione contro la modellizzazione dei fenomeni natutrali è che non si conoscono e non si possono valutare quantitativamente tutti i fattori in gioco nelle variazioni delle popolazioni. Tuttavia, è abbastanza acclarato che, in generale, in realtà non si presentano frequenti fattori veramente importanti e che spesso non vi sono più di 4 o 5 "fattori chiave", ed è proprio questo che permette la modellizzazione matematica.
1Sir Arthur Eddington (1882-1944)
2Albert Einstein (1879-1955)
3 N. David Mermin (1935-), Topological Theory of Defects in Review of Modern Physics, v. 51 n. 3, luglio 1979
4 Robert ed Ellen Kaplan, The Art of the Infinite, OUP 2003, p. 314.
 Quella qui proposta è una sintesi di quei concetti dell'analisi matematica che sono indispensabili per la comprensione dei concetti fisici legati all'insegnamento delle tecnologie farmaceutiche. Sebbene questa sintesi non abbia - e non potrebbe essere diversamente - alcuna pretesa di rigore formale e non possa sostituire i testi tradizionali, spero che abbia una impostazione didattica logica.
Quella qui proposta è una sintesi di quei concetti dell'analisi matematica che sono indispensabili per la comprensione dei concetti fisici legati all'insegnamento delle tecnologie farmaceutiche. Sebbene questa sintesi non abbia - e non potrebbe essere diversamente - alcuna pretesa di rigore formale e non possa sostituire i testi tradizionali, spero che abbia una impostazione didattica logica. 
 Moltissime teorizzazioni della matematica NON sono state ottenute dai matematici carpendole dall'albero della conoscenza, ma sono state prima abbozzate da persone spinte dalla necessità di risolvere problemi pratici, e poi riviste e approfondite in modo formale. Dunque, se questo è il naturale processo della mente umana, non si capisce per quale ragione nell'insegnare la matematica si debba percorrere il cammino inverso, come se la teoria fosse nata per prima. Come introduzione è preferibile sviluppare un percorso didattico che per quanto possibile ricostruisca proprio la genesi storica degli strumenti matematici.
Moltissime teorizzazioni della matematica NON sono state ottenute dai matematici carpendole dall'albero della conoscenza, ma sono state prima abbozzate da persone spinte dalla necessità di risolvere problemi pratici, e poi riviste e approfondite in modo formale. Dunque, se questo è il naturale processo della mente umana, non si capisce per quale ragione nell'insegnare la matematica si debba percorrere il cammino inverso, come se la teoria fosse nata per prima. Come introduzione è preferibile sviluppare un percorso didattico che per quanto possibile ricostruisca proprio la genesi storica degli strumenti matematici.

 L'albergatore sposterà tutti i clienti nella camera successiva (l'ospite della 1 alla 2, quello della 2 alla 3, etc.); in questo modo, benché l'albergo sia pieno è comunque, essendo infinito, possibile sistemare il nuovo ospite.
Immaginiamo ancòra che successivamente arrivi un'astronave con un numero infinito di nuovi ospiti.
L'albergatore sposterà tutti i clienti nella camera successiva (l'ospite della 1 alla 2, quello della 2 alla 3, etc.); in questo modo, benché l'albergo sia pieno è comunque, essendo infinito, possibile sistemare il nuovo ospite.
Immaginiamo ancòra che successivamente arrivi un'astronave con un numero infinito di nuovi ospiti.
 Il problema è formulato in questo modo: Achille si muove con velocità V, la tartaruga con velocità v, tali che V > v. La tartaruga parte rispetto ad Achille con un vantaggio che possiamo quantificare con una distanza, d. Il tempo che Achille impiegherà a raggiungere la posizione di partenza della tartaruga sarà dato da:
Il problema è formulato in questo modo: Achille si muove con velocità V, la tartaruga con velocità v, tali che V > v. La tartaruga parte rispetto ad Achille con un vantaggio che possiamo quantificare con una distanza, d. Il tempo che Achille impiegherà a raggiungere la posizione di partenza della tartaruga sarà dato da:
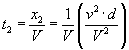
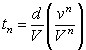

 In una sequenza markoviana, i cambiamenti di un sistema tra il tempo t e il tempo t +1 dipendono unicamente dallo stato nel tempo t. Però in natura, questi cambiamenti possono dipendere dallo stato del sistema in t -1. Per esempio, il tempo di domani dipende da quello di oggi, che a sua volta dipende da quello di ieri. Certo, detta così sembra contraddire quello che abbiamo detto a proposto del gioco dell'oca. Però, la cosa è chiara se pensiamo che certi fattori esercitano la loro azione con molto ritardo, per es. i cambiamenti meteorologici.
In una sequenza markoviana, i cambiamenti di un sistema tra il tempo t e il tempo t +1 dipendono unicamente dallo stato nel tempo t. Però in natura, questi cambiamenti possono dipendere dallo stato del sistema in t -1. Per esempio, il tempo di domani dipende da quello di oggi, che a sua volta dipende da quello di ieri. Certo, detta così sembra contraddire quello che abbiamo detto a proposto del gioco dell'oca. Però, la cosa è chiara se pensiamo che certi fattori esercitano la loro azione con molto ritardo, per es. i cambiamenti meteorologici.