Una velocità media di 117 km/h, tenendo conto di presumibili rallentamenti per code e magari lavori di manutenzione stradale, segùite da accelerazioni per raggiungere la "velocità di crociera", porta a supporre che non sia garanzia di una guida rispettosa dei limiti di velocità. Infatti, l'automobilista si vanta di aver percorso un tratto di 400 km in 2 h. In conclusione, la media calcolata è decisamente "appiattita": non fornisce alcuna indicazione delle valocità massima e minima.
Per ottenere una stima più precisa della velocità reale, occorre considerare percorsi più brevi, oppure tempi di rilevazione minori.
Per il nostro scopo (fig. 2), riportiamo su un diagramma le distanze percorse ai vari periodi di tempo: t1 = 0, t2 = 3 h, t3 = 5 h, t4 = 7 h
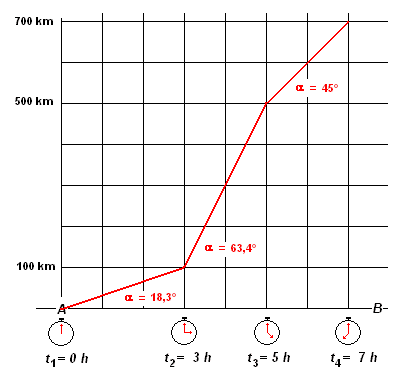 fig. 2 - distanze percorse a velocità costante e rilevate ad intervalli di tempo diversi |
Le velocità raggiunte nei singoli tratti, sono rispettivamente:
Infatti, in 3 h, procedendo alla velocità costante di 33,3 km/h, si percorre la distanza di 100 km; in 2h, procedendo alla velocità costante di 200 km/h, si percorre la distanza di 400 km; in 2h procedendo alla velocità costante di 100 km/h, si percorre la distanza di 200 km.
Questo significa che il diagramma spazio-tempo contiene, sebbene non esplicitamente, informazioni sulla velocità.
In particolare, osservando il diagramma, si nota che i vari tratti del percorso sono coperti in tempi diversi, e pertanto le semirette che collegano i punti a velocità costante (33,3 km/h; 200 km/h; 100 km/h), hanno pendenza differente: la semiretta più ripida si riferisce alla velocità media maggiore.
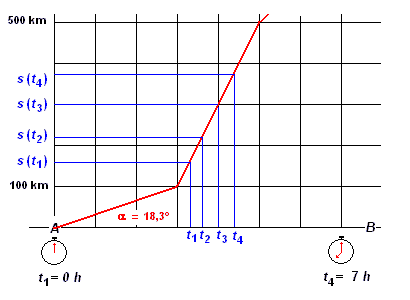 fig. 3 - un diagramma spazio-tempo fornisce implicitamente informazioni sulle velocità. |
Nel punto precedente, abbiamo visto che il diagramma spazio-tempo fornisce implicitamente informazioni sulla velocità. Nel caso di oggetti che si muovono a velocità costante, come nel tratto fra 100 e 500 km riportato nel diagramma di fig. 3, la velocità data dal rapporto spazio/tempo è uguale in qualsiasi intervallo di tempo, per esempio, tra t1 , t2 e t3 , t4 :
Nel caso più generale di un oggetto che si muove senza soste a velocità variabile (supponendo di aver effettuato un elevato numero di rilevazioni in modo da poter tracciare con elevata precisione il diagramma dei percorsi in funzione del tempo), la rappresentazione sarebbe verosimilmente una curva del tipo in figura 4.
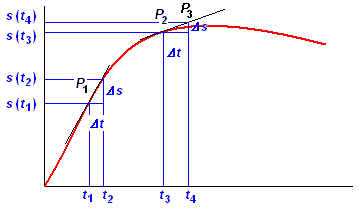 fig. 4 - diagramma spazio-tempo per un oggetto che si muove a velocità variabile |
Il problema che ci proponiamo di risolvere è se la velocità dell'oggetto in P1 è maggiore, minore o uguale alla velocità in P2
Per risolvere questo problema, è sufficiente tracciare con un righello le tangenti nel punto P1 e nel punto P2: la tangente con maggior pendenza corrisponde alla velocità maggiore in quanto, a parità di intervallo di tempo, viene percorsa una distanza maggiore. Osservando la figura 4, appare evidente che la tangente nel punto P1 ha una pendenza maggiore di quella nel punto P2.
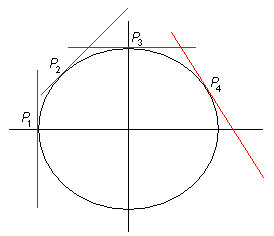
Nella figura a destra, sono tracciate le pendenze nei punti P1, P2, P3, P4 : si vede immediatamente che sono rispettivamente infinita (retta parallela all'asse y), positiva (retta con pendenza nel verso delle ascisse crescenti), nulla (retta parallela all'asse x), negativa (retta con pendenza nel verso delle ascisse decrescenti).
In effetti, la soluzione del problema proposto, è apparentemente banale; tuttavia, non è realmente soddisfacente in quanto presenta due difficoltà:
La soluzione corretta per la determinazione della tangente in un punto, viene ottenuta analiticamente. Per far questo, è sufficiente controllare se:
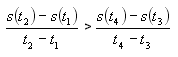
cioè, se la pendenza nel punto P1 è maggiore di quella nel punto P2.
In realtà, questo confronto non è del tutto rigoroso in quanto, osservando il diagramma di fig. 4, si vede che la pendenza nel punto P2 è approssimata: infatti è la pendenza fra il punto P2, ed il punto P3.
In effetti, la pendenza è definita come il rapporto tra il dislivello tra due punti Δy e la distanza Δx che li separa. Per conseguenza la pendenza in un punto, essendo nulla la distanza tra i due punti (coincidenti) tra cui è calcolata, implica che il rapporto Δy/ Δx = infinito, e dunque la tangente dovrebbe essere sempre parallela all'asse delle y.
Il problema trova soluzione osservando che la distanza tra i due punti di cui si vuole calcolare la pendenza non deve necessariamente essere nulla: è sufficiente che sia molto piccola, ma non nulla. L'animazione a destra mostra come, via via che la distanza Δx → 0, l'ipotenusa del triangolo di cateti Δy e Δx ruota attorno al punto di cui si vuol trovare la pendenza, fino a coincidere con la tangente in quel punto.
Esaminando ancóra il diagramma di fig. 2, si osserva che le tangenti sono uniche per ogni tratto percorso a velocità costante. Il valore della tangente in detti tratti è costante ed infatti in ogni tratto la velocità è costante.
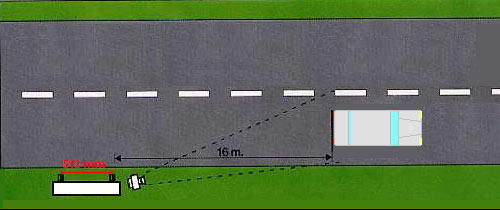
Il principio operativo del sistema autovelox (velomatic 512) si basa sulla misura dell'intervallo di tempo necessario ad un veicolo per transitare davanti agli assi geometrici dei due sensori che sono posti alla distanza di 512 mm (la parte anteriore del veicolo raggiunge il primo sensore e poi il secondo). Il piccolo intervallo di tempo Dt così misurato viene elaborato e trasformato in una indicazione numerica che rappresenta la velocità del veicolo espressa in km/h.
La fotocamera (che riprende la targa se la velocità del veicolo supera un valore fissato) viene posizionata nello stesso punto del rilevatore, l'apparecchiatura calcola la velocità del veicolo e scatta la fotografia quando la parte posteriore del veicolo si trova a 16 metri dal rilevatore. La circostanza di scattare il fotogramma sempre alla distanza di 16 metri dal rilevatore consente di poter identificare con esattezza il veicolo che ha commesso l'infrazione.
esempio: un'autovettura ha impiegato 0,013 sec per essere rilevata dal secondo sensore. La velocità è 0,512 m/0,013 sec = 141,7 km/h.
La scheda tecnica del velomatic 512 prevede un intrevallo di misura fra 3 e 999 km/h; la fotocamera ha una esposizione automatica a priorità di tempi a partire da 1/2000 sec ... se montate un motore jet sulla vostra vettura non verrete rilevati!
Applicando la definizione di rapporto incrementale, cioè quello riportato nella formula seguente e poi riproposto con esempi applicativi, si ha:
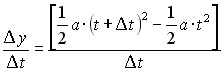
sviluppando i calcoli e semplificando, si ottiene:
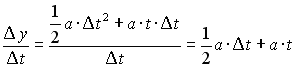
per ottenere la velocità in un generico punto P, occorre che l'intervallo di tempo, Dt sia prossimo a zero:
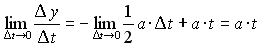
si faccia attenzione al fatto che prima di far tendera a zero l'incremento Δx, occorre sviluppare interamente il rapporto incrementale, altrimenti si resta con un... "pugno di mosche"!
Il risultato trovato, può essere espresso in forma generalizzata indicando con f '(x) la funzione derivata dalla f(x):
f(x) = a · x2 → f '(x) = 2 a · x
Più in generale, si dimostra che se l'esponente è n, risulta:
f(x) = a · xn → f '(x) = n a · xn-1
esempio 1: f(x) = 3 · x4 → f '(x) = 4 · 3 · x4-1 = 12 · x3
esempio 2: f(x) = 2/x = 2 · x-1 → f '(x) = -1 · 2 · x-1-1 = -2 · x-2 = -2/x2
Il pulsante rimanda ad un programma on-line per calcolare le derivate di una funzione:
f(x) = ex → f '(x) = ex
f(x) = e-x → f '(x) = e-x
f(x) = a·e-nx → f '(x) = -a·n· e-nx
f(x) = ln x → f '(x) = 1/x
f(x) = sen(x) → f '(x) = cos(x)
f(x) = cos(x) → f '(x) = - sen(x)
esempio: D (x3 + 2 x2) = 3x2 + 6x
esempio: D (x3 - 2 x2) = 3x2 + 6x
esempio: D (x3 · 2 x2) = 3x2 · 2x2 + 4x · x3
esempio: D (x3 / 2 x2) = (3x2 · 2x2 - 4x ·x3 )/4x4
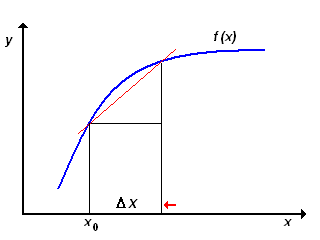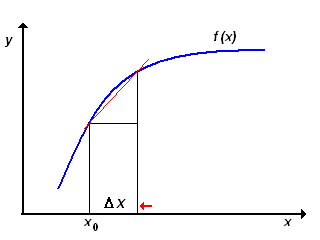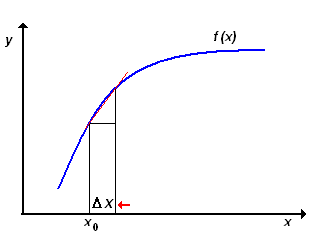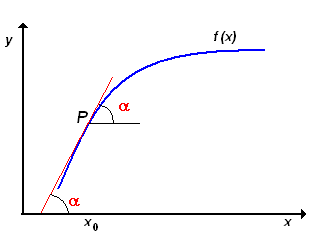
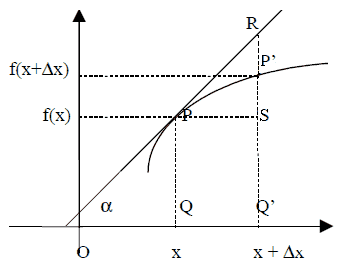Consideriamo, con riferimento alla figura a destra, una curva y = f(x) e i punti:
P [x, f (x)] ; P' [x + Δx , f (x + Δx) ] ; S [x + Δx, f(x) ]
Nel triangolo PSR si ha RS = PS · tg α = Δx f '(x)
dove: tg α = f '(x) per il significato geometrico di derivata
ora, quando la variabile indipendente passa da x a x + Δx , la funzione ha un incremento uguale alla lunghezza del segmento SP' .
Corrispondentemente, se consideriamo l'incremento rispetto alla retta tangente in P, si ha che tale incremento è RS , e questo è il differenziale della funzione in x.
Osservando attentamente la figura, è facile convincersi che quanto più l'incremento Δx è piccolo, tanto minore è la differenza fra il valore che assume la funzione nel punto x + Δx ed il valore del suo differenziale in quel punto.
Questa osservazione ci offre un risultato importante: invece di calcolare il valore di una funzione nel punto x + Δx , possiamo calcolare il valore del suo differenziale e la differenza, se Δx → 0 è praticamente trascurabile.
esempio: calcoliamo il valore della funzione f(x) = x2 quando la variabile indipendente passa da 2 a 2,1, cioè nel punto x = 2,1 :
f(2,1) = (2,1)2 = 4,41 e quindi l'incremento della funzione è 4,41 - 4 = 0,41
eseguiamo l'operazione con il differenziale. Il differenziale nel punto x = 2,1 è:
df(x) = f '(x) Δx = 2x Δx = 2(2,1) · 0,1 = 0,42
la differenza è apprezzabile, però se ripetiamo il calcolo per un incremento di 0,01 allora si può facilmente verificare che i risultati sono praticamente coincidenti:
f(2,01) = (2,01)2 = 4,04 e quindi l'incremento della funzione è 4,04 - 4 = 0.04
il differenziale nel punto x = 2,01 è:
df(x) = f '(x) Δx = 2x Δx = 2(2.01) · 0,01 = 0,04
esempio 2: calcoliamo il valore della funzione f(x) = x3 quando la variabile indipendente passa da 4 a 4,1, cioè nel punto x = 4,1 :
f(4,1) = (4,1)3 = 68,98 e quindi l'incremento della funzione è 68,98 - 64 = 4,98
eseguiamo l'operazione con il differenziale. Il differenziale nel punto x = 4,1 è:
df(x) = f 2,01'(x) Δx = 3x2 Δx = 3(4,1)2 · 0,1 = 5,04
la differenza è apprezzabile, però se ripetiamo il calcolo per un incremento di 0,01 allora si può facilmente verificare che i risultati (alla seconda cifra decimale) sono coincidenti:
f(4,01) = (4,01)3 = 64,48 e quindi l'incremento della funzione è 64,48 - 64 = 0.48
il differenziale nel punto x = 4,01 è:
df(x) = f '(x) Δx = 3x2 Δx = 3(4.01)2 · 0,01 = 0,48
data la funzione y = f(x) = x, allora df(x)= dy = f '(x) Δx ; essendo f '(x) = 1, si ha:
dy = 1 · Δx (eq. 1)
siccome la funzione considerata è y = x, segue che dy = dx e quindi, sostituendo nella (1), si ottiene: dy = dx = Δx
in definitiva il differenziale di partenza può scriversi:
dy = f ' (x) dx
la notazione df(x)/dx, usata per indicare la derivata, oltre ad un suo valore come simbolo in sé, ha un notevole valore pratico in quanto dimostra che:
la derivata è il quoziente tra il differenziale della funzione e quello della variabile.
Questo significa che possiamo scrivere:
df(x) = f '(x) dx
con il risultato ottenuto, per esempio, possiamo affermare che le variazioni di concentrazione di una soluzione che si sta degradando secondo una cinetica da individuare sono proporzionali ad intervalli di tempo infinitesimi.
dc = f '(c) dt
dove f ' (c) possiamo supporre che - salvo verifica sperimentale- sia 0; k · c; k · c2 ; ecc.
questo significa che possiamo modellizzare istante dopo istante la variazione di concentrazione che varia secondo una legge che non conosciamo, però conosciamo come dipende dal tempo la variazione infinitesima di concentrazione. La variazione di concentrazione in funzione del tempo, come vedremo nel seguito, si troverà risolvendo un'equazione differenziale.
 |
2 | 3 |
4 |
5 |
6 |
7 |
8 |
| HOME PAGE |
|||||||
Marcello Guidotti, copyright 2011