antiderivate

Gli esempi che seguono, dimostrano che questo calcolo, nel caso delle derivate fondamentali, è immediato:

Poichè la derivata, D, di a xⁿ è:

D a xⁿ = n a x^n-1

è facile vedere che l'antiderivata, D^-1, è:

D ^-1 n a x^n-1

si calcola aumentando di un'unità il numero ad esponente e dividendo tutto per n:

D ^-1 n a x^n-1 = 1/n a n x^{n-1 + 1} = a x ⁿ + c

esempio: calcolare l'antiderivata di x³/2 → x⁴/2·4

esempio: calcolare l'antiderivata di 1/x² = x^-2 →x^-2+1/(-1) = -1/x + c

Ad ogni antiderivata è necessario addizionare una costante generica, c, in quanto operando di nuovo l'operazione di derivata, la costante sparisce.
esempio: D x³ + 2 = 3 x, ma anche D x³ + c = 3 x

La regola appena ricordata non vale nel caso di 1/x .
Infatti, applicando la regola si otterrebbe: x^{-1 +1}/(-1 + 1), cioé una forma indefinita.
Pertanto, occorre procedere come spiegato appresso.

Ricordando che la derivata di ln x

D ln x = 1/x

è facile riconoscere che:

D^-1 (1/x) = ln x + c

Ancóra un esempio:

poiché la derivata di sen x è:

D sen x = cos x

è facile riconoscere che:

D^-1 sen x = - cos x

Quando la funzione di cui si vuole calcolare l'antiderivata non è una funzione facilmente riconoscibile, si ricorre a metodi per ricondurla ad una combinazione di derivate fondamentali. I procedimenti in questione esulano dalle finalità di questi richiami di matematica e quindi il lettore interessato è invitato a consultare un qualsiasi testo di analisi matematica.

Per ragioni che verranno chiarite nella prossima pagina, la notazione di antiderivata
non è indicata come D^-1 f(x), bensì come ∫ f(x) dx (il simbolo a forma di "S" allungata è detto operatore integrale) e l'operazione da effettuare prende il nome di integrazione

Il pulsante rimanda ad un programma on-line per calcolare le antiderivate di una funzione:

equazioni differenziali

1. conoscendo una funzione trovare la sua derivata e il suo differenziale (derivazione);
2. conoscendo una derivata o un differenziale ritrovare la funzione (integrazione);
3. conoscendo una relazione fra una funzione, la sua variabile e le sue derivate, trovare la funzione incognita che la soddisfa (soluzione di un'equazione differenziale).

In generale, per risolvere le equazioni differenzieli è utile trattare la derivata con la notazione di Leibnitz, cioé come rapporto tra differenziali.

esempio 1: df(x)/dx = 0 in questo caso la funzione f(x) è costante

infatti se f(x) = cost → df(x)/dx = 0

esempio 2: la velocità con cui viene eliminato un farmaco dal corpo e quindi si riduce la concentrazione ematica, c, nel tempo, t, è data dall'equazione:

dc/dt = -kc

in questo caso, abbiamo la funzione c, la variabile t e la derivata dc/dt . Dunque è un'equazione differenziale.

La soluzione della (1) si ottiene per separazione di variabili:

dc/c = -kdt integrando si ottiene ln c = -kt + costante

la costante si calcola ponendo t = 0 e fornisce la concentrazione al tempo iniziale

ln c₀ = costante

e dunqua l'equazione differenziale ha per soluzione:

ln c = -kt + ln c₀

esempio 3: la velocità al tempo t di un corpo che si muove di moto uniformemente accelerato è data da:

v = ds/dt = a · t

separando le variabili:

ds = a · t dt → s = a t²/2

cioé lo spazio percorso da un corpo che si muoave di moto uniformemente accelerato.

equazione dell'assorbimento-eliminazione per un farmaco somministrato oralmente

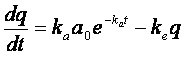        (1)

è un'equazione differenziale lineare a coefficienti costanti. Di séguito è riportato il metodo di soluzione:

si pone q = u · v, due variabili di comodo e si calcola la derivata rispetto a t:

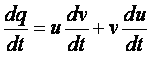        (2)

la derivata (2) si sostituisce nel primo membro della (1):

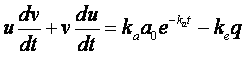        (3)

si sostituisce nella (3) q con u·v

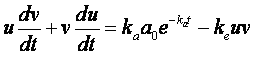        (4)

si raggruppano le variabili comuni:

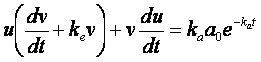        (5)

si determina la funzione che annulla il termine in parentesi a primo membro:

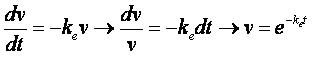        (6)

se il termine in parentesi è nullo, la (5) diventa:

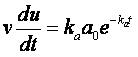        (7)

sostituendo nella (7) v = exp(-k_et),

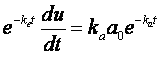        (8)

raggruppando:

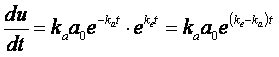        (9)

separando le variabili:

        (10)

integrando:

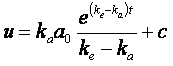        (11)

per ottenere q, occorre moltiplicare per v = exp(-k_et):

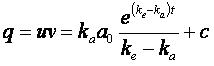        (12)

A questo punto, si dovrebbe determinare il valore della costante, c, il cui calcolo è tralasciato in quanto risulta piuttosto laborioso senza aggiungere molto ai fini di questa presentazione.

	2	3	4	5	6	7	8
HOME PAGE

Marcello Guidotti, copyright 2011