decrescente verso l'alto permette di ottenere un cono.
Democrito di Abdera (460? - 360?a.C.) in base citazioni fatte da autori successivi (ad esempio, Archimede), fu il primo ad enunciare il teorema che afferma che il volume di un cono è un terzo di quello di un cilindro di uguale altezza, e che quello di una piramide è un terzo di quello di un prisma di uguale altezza. La cosa interessante è che Democrito abbia utilizzato metodi "infinitesimali" .
Plutarco (46 - 127 a.C.) cita un paradosso attribuito a Democrito anch'esso riguardante problemi di "infinitesimi": se un cono fosse tagliato con piani paralleli alla sua base [infinitamente vicini alla base stessa], cosa dovremmo pensare delle superfici che formano le sezioni ottenute? Sarebbero uguali fra loro o no? Perché se fossero disuguali, allora renderebbero il cono irregolare, indentato, come a gradini, e non liscio; ma, se fossero uguali, allora il cono avrebbe la proprietà del cilindro e sarebbe formato da sezioni circolari uguali e non diverse, il che è assurdo.
Ci sono aspetti importanti in questo paradosso in cui Democrito pensa un solido come composto dalle sue (infinite) sezioni piane, e (come ci dice Archimede) può aver usato questa idea per dimostrare uguaglianze fra volumi di solidi diversi, anche se l'enunciare questo paradosso pare mostrare che già Democrito stesso cogliesse gli aspetti problematici di questo tipo di procedure (la somma di infiniti triangoli di volume zero non ha volume zero?).
 |
| la sovrapposizione di dischi con raggio via via decrescente verso l'alto permette di ottenere un cono. |
Come si vede, in entrambi concetti siamo costretti a far intervenire l'idea di infinito: come infinita divisibilità nel primo caso, come infinito numero degli indivisibili (atomi, monadi o punti, come verranno chiamati) che formano gli enti geometrici e fisici, ed anche nel concetto di infinitesimo che ad essi si verrebbe ad attribuire.
Zenone, con il paradosso detto dei Molti, osservò che che se gli "atomi" non hanno grandezza (dimensione, estensione, lunghezza, volume), ovverosia se hanno grandezza zero, allora per quanti se ne sommino avremo sempre grandezza zero, quindi non potrebbe esistere nulla di misura diversa da zero. Se invece gli atomi hanno estensione non nulla, si ottiene un'altra contraddizione: ogni grandezza deve essere formata da un numero infinito di atomi (poiché la scoperta della incommensurabilità ha mostrato che supporre le grandezze formate da un numero finito di atomi porta a contraddizione), ma un numero infinito di grandezze finite non nulle mi darebbe una grandezza infinita, e quindi tutte le grandezze dovrebbero essere infinite. Perciò entrambe le ipotesi portano ad una contraddizione.
Qui, il problema nasce con l'identificazione dei punti astratti che compongono un segmento tracciato a matita su un foglio, con il numero di atomi di grafite che formano il segmento: il segmento matematico è costituito da numeri, il segmemto di grafite è costituito da atomi.
Scrive Bertrand Russell (Introduzione alla filosofia matematica, traduzione italiana Roma, Newton & Compton Editori, 1997) :
"Non si può dire che sia sicuro che esista in realtà un qualsiasi insieme infinito nel mondo. L'ipotesi che esista è quello che noi chiamiamo l'assioma dell'infinito.
Sebbene esistano vari modi con i quali si potrebbe sperare di dimostrare questo assioma, c'è ragione di pensare che siano tutti errati, e che non vi siano ragioni logiche conclusive per ritenerlo vero. Nello stesso tempo, non esistono ragioni logiche 'contro' gli insiemi infiniti, e siamo pertanto logicamente autorizzati a esaminare l'ipotesi che esistano tali insiemi. (...)"
Pertanto, alla domanda che ci eravamo posta: «se esista, al mondo, qualche cosa di infinito», dobbiamo rispondere che certamente esiste in senso logico-matematico; ma che, in senso fisico e materiale, non possiamo affermarlo né negarlo.
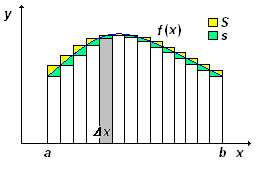 considerando per un dato intervallo Dx, la sua ordinata minima e moltiplicandola per l'intervallo, si ottiene un rettangolo di area minore (per la parte in verde) dell'area sottesa dalla curva in detto intervallo. Se si considera l'ordinata massima, si ottiene un rettangolo di area maggiore (parte in giallo) dell'area sottesa dalla curva. |
Ci proponiamo di determinare l'area A sottesa dalla curva f(x). A tal fine, dividiamo l'intervallo b - a = d in un numero n di segmenti uguali, e dai punti di divisione tracciamo delle perpendicolari all'asse delle x fino ad incontrare la curva. Queste perpendicolari dividono la regione della quale desideriamo determinare l'area in n stretti rettangoli verticali. Ognuno di questi rettangoli ha area pari a:
dove:
f(xi) = altezza del rettangolo a distanza xi dall'origine;
Dx = d/n
Indicando con xi la coordinata orizzontale di ogni singolo intervallo Dx, si ha:
| (1) | 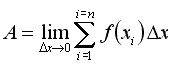 |
Le altezze per le quali devono essere moltiplicati gli intervalli Dx, possono essere scelte fra quella minima e quella massima. Scegliendo sempre l'altezza minima, si ottiene un'area Amin < A; scegliendo sempre l'altezza massima, si ottiene un'area Amax > A. E' intuitivo che se Dx ![]() 0, Amin = Amax, e dunque si ottiene l'area A.
0, Amin = Amax, e dunque si ottiene l'area A.
Per esaminare un'applicazione semplice della (1), ci proponiamo di calcolare l'area sottesa da una parabola, di equazione y = x2 nell'intervallo [0, 1] diviso in intervalli di 0,1
area = [(0)2 + (0,1)2 + (0,2)2 + (0,3)2 + ... + (0,9)2 + (1)2 ] · 0,1 = 0,385

come si vede, il calcolo tramite sommatoria è piuttosto laborioso e non è sempre agevole determinare il termine generale di una serie e calcolarne il limite. Così, questo procedimento, sebbene corretto, non sembra offrire concreti vantaggi rispetto al calcolo di un'area mediante pesata (in pratica si ritaglia dal foglio ove è disegnata la figura di cui si vuole trovare l'area e la si pesa. Sapendo il peso di un foglio, con una proporzione si risolve il problema).
La scoperta di metodi generali di risoluzione non avvenne tutta in una volta, bensì fu il frutto del lavoro collettivo di molte generazioni; infatti, il concetto della divisione in un numero infinitamente grande di termini infinitamente piccoli era conosciuto da tempo, tanto che era familiare ai matematici dell'antica Grecia. Ad esempio, Archimede (287-212 a.C.) seppe calcolare il volume di una sfera e di un cono. Poi, durante il medioevo, il pensiero scientifico attraversò un periodo di profondo declino e fu solo agli inizi del sedicesimo secolo che le scienze (e, in particolare le matematiche) iniziarono un nuovo profondo sviluppo. I risultati dei Greci vennero inizialmente ripresi, ed a questi seguirono nuove conquiste. In particolare, nuovi sviluppi si verificarono per le somme di grandezze infinitamente piccole. Questo metodo ricevette un grande impulso dalle opere di Kepler e di B. Cavalieri. Tuttavia, questi due autori non erano riusciti ad individuare un metodo generale per calcolare i limiti delle somme.
Questi metodi assunsero la loro forma attuale grazie ai lavori di G. W. Leibnitz (1646-1716) e I. Newton (1642-1727). Il termine integrale deriva dalla scuola di Leibnitz e fu introdotto nell'anno 1690.
La soluzione del problema generale del calcolo delle aree, come si è detto, è dovuta ad una successione di studi, che possono riassumersi su un'osservazione fondamentale.
Si considerino, per esempio, le aree sottese dalle seguenti funzioni e calcolate con la formula (1):
sembrerebbe quindi che l'area sottesa da una funzione f(x) sia uguale, a meno di una costante, alla sua antiderivata. Si tratta di verificare se questa ipotesi è vera in generale, e ne daremo dimostrazione nel prossimo paragrafo.
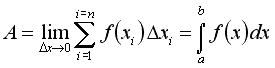

A questo punto è evidente che il problema del calcolo dell'area non è ancóra risolto. Abbiamo solo indicato un simbolo (una "S" allungata) per un nuovo operatore che prende il nome di integrale. Così, per risolvere completamente il problema, dobbiamo trovare un modo generale per stabilire quale operazione si deve associare all'operatore.
un operatore è il simbolo con il quale indichiamo una determinata operazione. Per es., "+" è l'operatore di somma; "log" è l'operatore per il logaritmo.
Il metodo di ricerca delle tangenti sviluppato da Isaac Barrow (matematico e teologo inglese, 1630-77), anticipò il calcolo differenziale sviluppato da Isaac Newton. Barrow fu professore di matematica a Cambridge dal 1663 al 1669 ed a lui succedette Newton. Sebbene Barrow non enunciò mai esplicitamente i teoremi fondamentali del calcolo, ne anticipò i risultati e Newton continuando in quella direzione ne enunciò esplicitamente i teoremi. Per un doveroso omaggio ai lavori di Torricelli e Barrow, si è soliti ricordare con il loro nome il teorema fondamentale del calcolo integrale.
Iniziamo con l'osservare che il valore dell'integrale (1) varia al variare dell'estremo superiore b. Pertanto, converremo di indicare il valore dell'area A come:
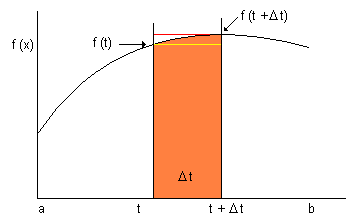
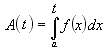
Se f(x) è una funzione non negativa, allora A(x) è contenuta nel primo quadrante ed ha per valore numerico l'area del trapezoide colorata in arancio: questa area varia con t ed è A(t + Δt)-A(t)
Ciò premesso, l'area del trapezoide è minore di quella del rettangolo il cui estremo superiore è definito da una linea rossa, f(t + Δt) Δt ed è maggiore di quella del rettangolo il cui estremo superiore è definito da una linea gialla f(t) Δ t :
dividendo i tre membri per Δt , si ottiene:
se Δ t → 0 , allora il termine a secondo mebro è la derivata dell'area, A (t); il termine al terzo membro coincide con il primo e siccome quest'area deve essere maggiore del termine a primo membro e minore di quello a secondo membro, si deve avere l'identificazione con questi ultime due:
dunque: la derivata della funzione integrale, A(t), in un punto, t, è uguale al valore che la funzione integranda assume in quello stesso punto.

In termini pratici, poiché il teorema di Torricelli-Barrow dimostra che la funzione integrale e il suo integrale non sono due funzioni indipendenti, l'area sottesa da una funzione f (x), si può ricondurre alla ricerca di una funzione primitiva F(x) la cui derivata è f (x).
(eq. 1) 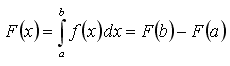 |
la (1) risolve completamente il problema dell'integrazione.
dimostrazione: consideriamo l'integrale:
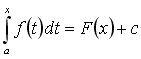
dove la costante c dipende dall'estremo inferiore, a.
Per determinare la costante c, consideriamo l'integrale:
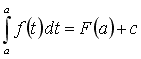
se osserviamo che gli estremi di integrazione coincidono, allora l'integrale deve essere nullo (l'area sottesa da una funzione su un intervallo nullo è nulla), e quindi. F(a) + c = 0, da cui - F(a) = c
sostituendo il valore della costante c nella (2) si ottiene:
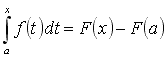
ponendo x = b, si ottiene la formula di Newton-Leibnitz.
Presa una retta orizzontale, potremo sempre spostarla verso l'alto o verso il basso in modo da realizzare la situazione in cui l'area del rettangolo compreso fra la retta e l'asse x, sull'intervallo [a, b], sia perfettamente uguale all’area del trapezoide.
L'ordinata costante dei punti di tale retta dovrà evidentemente essere compresa fra il minimo assoluto e il massimo assoluto della funzione su [a, b], quindi la retta sarà obbligata a tagliare la curva continua in almeno un punto. L'ascissa di tale punto di intersezione retta-curva è l'ascissa c di cui il teorema afferma l'esistenza.
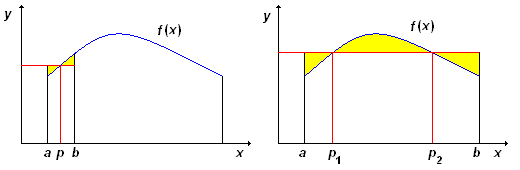
Data una qualsiasi funzione f(x), è sempre possibile individuare un intervallo [a, b], al cui interno esiste almeno un punto, p, per il quale si può condurre una retta parallela all'asse delle ascisse in modo da dividere in due parti uguali l'area compresa in parte sopra la curva ed in parte sotto la curva (v. colorazione in giallo)
in questo caso, si ha: A = f(p)(b-a)
| 5 | |||||||
Marcello Guidotti, copyright 2011