dati oggettivi, interpretazione soggettiva
Se ripetuta con sufficiente frequenza, una menzogna diventa la nuova verità.
Paul Joseph Goebbels, ministro della propaganda della Germania nazista |
Nella parte dedicata alla statistica descrittiva, abbiamo riportato una serie di statistiche costruite su campioni non correttamente raccolti e su dati interpretati in modo errato, spesso confondendo una connessione apparente con il reale responsabile di un'osservazione. Accanto a queste bizzarre conclusioni frutto di statistiche mal eseguite, vi sono statistiche corrette "spiegate" in modo bizzarro.
 Con il termine anglosassone spin doctor, si indica una persona esperta nel cosigliare altre persone (politici, manager, economisti, opinionisti) su come distorcere la verità, o se si preferisce, individuare all'interno di una raccolta di dati oggettivi un modo per renderli soggettivi... cioè presentarli secondo un certo punto di vista.
Con il termine anglosassone spin doctor, si indica una persona esperta nel cosigliare altre persone (politici, manager, economisti, opinionisti) su come distorcere la verità, o se si preferisce, individuare all'interno di una raccolta di dati oggettivi un modo per renderli soggettivi... cioè presentarli secondo un certo punto di vista.
la funzione dello spin doctor è di far apparire le notizie migliori (o peggiori) di quanto siano in realtà. In questo caso, non si tratta delle insidie intrinseche ad alcune statistiche, ma di evidenti forzature, agevolate dalla scarsa dimestichezza e volontà di controllo del fruitore.
la legge di Lavoisier
"In natura nulla si crea e nulla si distrugge, ma si trasforma solamente". Non sono le parole esatte con cui Lavoisier enunciò il risultato dei suoi studi, ma certamente ne racchiudono il senso. Ebbene, questa legge può essere elusa...
Consideriamo, per esempio, dati di vendita dell'azienda Socometicuro SpA che produce un medicinale OTC per il disturbo X. I resoconti relativi al fatturato forniscono 2 milioni di euro per il 2005 e 2 e 60.000 euro per il 2006. Certo, non è un granché, ma comunque indica un fatturato incrementato del 3 per cento. Non male in un periodo di modesto andamento dell'economia. I giornali, se l'azienda è di interesse rilevante, possono indicarla come un esempio di gestione efficace.
In realtà, i responsabili dell'immagine aziendale hanno tralasciato un piccolo dettaglio: l'inflazione tra il 2005 e il 2006 è stata del 3 per cento, corrispondente proprio all'aumento dei prezzi di vendita. In pratica, se i prezzi aumentano in misura uguale all'inflazione, il numero di pezzi venduti rimane invariato.
Ignorare il tasso di inflazione o i rapporti di cambio (in caso di confronti con valute diverse) è il primo trucco per fornire informazioni distorte.
è la somma che fa il totale (Totò Fabrizi e i giovani d'oggi)
Per contrastare l'aumento della spese per la tutela dell'ambiente, il comune X ha disposto una tassa locale che prevede un incremento di 15 euro sui rifiuti urbani per ognuno dei successivi 3 anni.
| bolletta annua odierna |
2 anno |
3 anno |
4 anno |
| 150 euro |
165 euro |
180 euro |
195 euro |
In termini percentuali, l'aumento complessivo di 45 euro rapportato alla bolletta media di 150 euro fornisce un valore del 30% (45/150 = 0,3). Un incremento certamente considerevole ma spaventoso, ben 90 euro, quando riferito dal nuovo candidato sindaco: per distorcere il dato è sufficiente considerare i singoli incrementi annuali... il secondo anno si pagheranno 15 euro in più dell'anno precedente; il terzo 30; il quarto 45. In totale 90 euro!
distribuzioni statistiche a confronto: medie mobili
Consideriamo le seguenti distribuzioni di dati i cui elementi si riferiscono, per esempio, a pezzi prodotti (in decine di migliaia) da un'azienda A che produce elettrodomestici di varia tipologia (per esempio, macchinetta per popcorn 40 mila, tostapane 40 mila, ..., microonde 60 mila, ... , frigoriferi 120 mila)


| 4, 4, 4, 4, 6, 6, 8, 10, 10, 12 |
media = 6.8 |
moda = 4 |
mediana = 6 |
Supponiamo che sul mercato esista l'azienda B, che produce un'analoga linea di prodotti concorrente, riassunta dai seguenti dati statistici:
| 2, 2, 2, 2, 4, 6, 6, 6, 8, 10 |
media = 4.8 |
moda = 2 |
mediana = 5 |
Ora supponiamo che l'azienza A, dopo aver acquisito il controllo azionario dell'azienda B, trasferisca la produzione di frullatori (40 mila pezzi) nell'azienda B. In questo modo i nuovi dati statistici dell'azienda A sono così modificati:
| 4, 4, 4, 6, 6, 8, 10, 10, 12 |
media = 7,1 |
moda = 4 |
mediana = 6 |
Dopo il trasferimento della produzione di frullatori, i nuovi dati statistici dell'azienda B sono così modificati:
| 2, 2, 2, 2, 4, 4, 6, 6, 6, 8, 10 |
media = 4.7 |
moda = 2 |
mediana = 4 |
E' facile vedere che in questo modo l'azienda A potrà comunicare stringatamente che dopo l'acquisizione del controllo dell'azienda B, una riorganizzazione delle linee produttive ha prodotto sinergismi con una variazione delle medie produttive che sono passate da 6.8 a 7.1 per la controllante (A) a fronte di una diminuzione da 4.8 a 4.7 per la controllata (B). D'altra parte, l'incremento netto (aumento della media produttiva controllante - controllata) = 4.4% - 2% = 2.4%
In realtà, i dati di quello che è/sembra un gioco di prestigio si riferiscono solo ad un dato statistico e non c'è alcuna informazione su quello che sarà il prossimo reale andamento economico delle due aziende. Comunque, un esame delle tabelle, evidenzia come la mediana dell'azienda B si sia spostata verso sinistra: un aumento dei dati che sono nella parte sinistra della media. In altre parole, la ricchezza totale delle due aziende è rimasta invariata; è uicamente cambiata la sua distribuzione.
ovvietà... o no?
 Il direttore marketing di un'azienda farmaceutica, riferendo un comunicato aziendale, coglie l'occasione per uno sprone:
Il direttore marketing di un'azienda farmaceutica, riferendo un comunicato aziendale, coglie l'occasione per uno sprone:
Sono abbastanza soddifatto di comunicare che quest'anno la metà dei nostri informatori ha raggiunto obiettivi superiori alla media; d'altra parte, questo significa che la metà degli informatori dovrà aumentare la sua efficienza.
Nella definizione statistica della media, quanto affermato dal comunicato aziendale non fornisce alcuna informazione: essendo la media un indicatore intermedio, ci sarà necessariamante una parte di elementi che otterrà valori superiori o inferiori alla media, a prescindere dalla qualità dei loro risultati.
il paradosso di Simpson
Nel 1934 due ricercatori statunitensi esaminando dati del 1910, relativi a decessi per tubercolosi nelle città di New York e Richmond, osservarono questo singolare paradosso:
mortalità del ceppo afroamericano a Richmond < mortalità del ceppo afroamericano a New York;
mortalità del ceppo caucasico a Richmond < mortalità del ceppo caucasico a New York.
Aggregando i dati, il risultato si invertiva: la mortalità complessiva dei due ceppi era maggiore a Richmond rispetto a New York...
Questo paradosso di inversione statistica è noto come paradosso di Simpson che lo descrisse nell'articolo The interpretation of interaction in contingency tables nel Journal of the Royal Statistical Society (1951). Ed una sua breve disamina permette di chiarire l'importanza di applicare test statistici prima di formulare conclusioni.
Supponiamo, per esempio, che due studi indipendenti per provare l'efficacia di un farmaco A rispetto ad un farmaco B abbiano dato i risultati riassunti nelle due tabelle che seguono.
|
guariti |
non guariti |
|
| farmaco A |
60 |
15 |
75 |
| farmaco B |
45 |
20 |
65 |
|
105 |
35 |
140 |
|
guariti |
non guariti |
|
| farmaco A |
95 |
90 |
185 |
| farmaco B |
5 |
10 |
15 |
|
100 |
100 |
200 |
|
Ora, calcoliamo le percentuali di guariti riportate dal primo studio:
farmaco A = 60/75 = 0,8 ; farmaco B = 45/65 = 0,69
le percentuali di guariti riporate dal secondo studio danno:
farmaco A = 95/185 = 0,51 ; farmaco B = 5/15 = 0,33
E' ovvio concludere che il farmaco A è più efficace del farmaco B. Ovvio?
Ora, calcoliamo le percentuali dei guariti con il farmaco A sommando i risultati dei due studi: (60 + 95)/(75 + 185)= 0,60
calcoliamo le percentuali dei guariti con il farmaco B sommando i risultati dei due studi: (45 + 5)/(65 + 15) = 0,62
Il farmaco B è più efficace del farmaco A, o comunque la differenza di efficacia sembra irrilevante.
|
guariti |
non guariti |
|
| farmaco A (totale) |
155 |
105 |
260 |
| farmaco B (totale) |
50 |
30 |
80 |
|
205 |
135 |
340 |
Questo risultato paradossale, che illustra un errore che può facilmente presentarsi nella statistica medica, trova una spiegazione nel fatto che aggregando dati ottenuti da sperimentazioni diverse, non si considerano elementi che, se esplicitati, avrebbero evidenziato differenze tra i due campionamenti (per es. differente percentuale di uomini e donne, differenze di peso, ecc.).
Come vedremo nella parte dedicata alla statistica inferenziale, con l'applicazione di tecniche di campionamento corrette, unitamente all'uso di test statistici può ridursi la possibilitÓ d'interpretazioni "fantasiose".
il fattore d'inganno
I grafici si basano sulla nostra capacità di visualizzare i numeri associandoli alle dimensioni di alcune immagini. La rappresentazione dei numeri, come misure fisiche, sulla superficie di un grafico, dovrebbe essere direttamente proporzionale alla quantità geometriche rappresentate. La violazione di questo criterio è misurata dal "fattore d'inganno", definito come il rapporto della misura di un effetto mostrato su un grafico e le misura dello stesso effetto in forma numerica.
Il fatto che i grafici o le immagini siano comunque accompagnati dai corretti dati numerici, è irrilivante in quanto il fruitore di un testo tende a ricordare le immagini piuttosto che i dati.
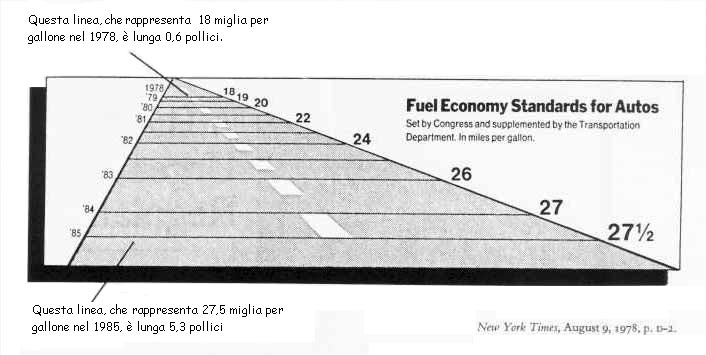
Questo grafico, pubblicato sul New York Times, ha lo scopo di mostrare il mandato dell'economia dei carburanti secondo gli standard del Dipartimento dei Trasporti. Gli standard richiedono un incremento nelle percorrenze da 18 a 27.5 miglia per gallone (3.78l L) (da 7.6 a 11,5 km/l), con un incremento del 53%. La grandezza dell'incremento mostrata nel grafico è il 783% per un fattore d'inganno colossale = (783/53)=14.8!
 Un altro elemento chiave nel produrre grafici informativi è evitare di confondere le variazioni negli elementi del disegno con le variazioni dei dati. Ciò comporta che i cambiamenti nella scala dei grafici dovrebbero sempre corrispondere ai cambiamenti dei dati da rappresentare. Questo grafico vìola questo principio usando le dimensioni dei medici per mostrare dati mono-dimensionali, dando un fattore di inganno (2.8) più contenuto rispetto al caso precedente.
Un altro elemento chiave nel produrre grafici informativi è evitare di confondere le variazioni negli elementi del disegno con le variazioni dei dati. Ciò comporta che i cambiamenti nella scala dei grafici dovrebbero sempre corrispondere ai cambiamenti dei dati da rappresentare. Questo grafico vìola questo principio usando le dimensioni dei medici per mostrare dati mono-dimensionali, dando un fattore di inganno (2.8) più contenuto rispetto al caso precedente.
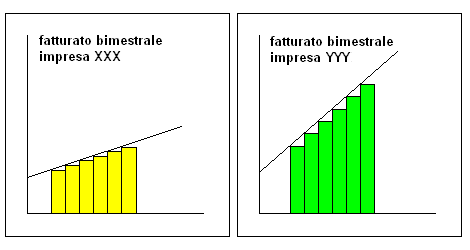 Una variante del fattore di scala è si ottiene modificando la scala delle ordinate in modo da ottenere una pendenza differente. I due istogrammi riportano i fatturati e quindi la penetrazione commerciale delle aziende XXX e YYY. Scegliendo opportunamente la scala delle ordinate, si può suggerire che l'azienda YYY abbia un incremento di fatturato maggiore.
Una variante del fattore di scala è si ottiene modificando la scala delle ordinate in modo da ottenere una pendenza differente. I due istogrammi riportano i fatturati e quindi la penetrazione commerciale delle aziende XXX e YYY. Scegliendo opportunamente la scala delle ordinate, si può suggerire che l'azienda YYY abbia un incremento di fatturato maggiore.
Un'altra possibilità si presenta con i diagrammi a torta:
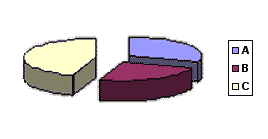
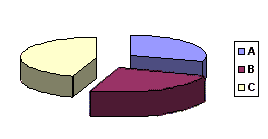 Il diagramma a torta a sinistra, mostra una ripartizione A = 30; B = 25; C = 45; anche quello a destra mostra la stessa ripartizione; tuttavia, la "fetta" C è stata portata in primo piano... sebbene A sia maggiore di B, l'occhio percepirà B come maggiore e la forza dell'immagine si sovrapporrà al dato numerico: B sembrerà realmente maggiore di A e forse anche di C!
Il diagramma a torta a sinistra, mostra una ripartizione A = 30; B = 25; C = 45; anche quello a destra mostra la stessa ripartizione; tuttavia, la "fetta" C è stata portata in primo piano... sebbene A sia maggiore di B, l'occhio percepirà B come maggiore e la forza dell'immagine si sovrapporrà al dato numerico: B sembrerà realmente maggiore di A e forse anche di C!
Mettendo al posto di A, B, C un nome e lasciando i dati numerici nel corpo del testo, si avrà un'informazione corretta, ma sarà evidenziata la fetta B.
contesto: riferito a cosa?
La correttezza dell'informazione richiede che un grafico non debba mostrare dati fuori contesto, e significativi confronti, visivamente evidenziati, dovrebbero essere fatti su basi uguali - ceteris paribus - in modo che tutte cose rimangano uguali.
Quando lo scopo di un grafico è permettere il confronto, o mostrare differenze tra i casi, la questione da chiedere è: "confrontato con cosa?"
E' facile evitare l'importante, utile o rilevante confronto separandoli visivamente, o fabbricando banali relazioni più promettenti.
 Questo grafico, proveniente da Social Indicators III, si propone di confrontare le tendenze nei redditi mediani di uomini e donne per livello d'istruzione. Ma impilando i grafici degli uomini e delle donne verticalmente, si nasconde la maggior redditività. Lo stiramento della scala orizzontale aiuta anche a nascondere quelsiasi tendenza futura.
Questo grafico, proveniente da Social Indicators III, si propone di confrontare le tendenze nei redditi mediani di uomini e donne per livello d'istruzione. Ma impilando i grafici degli uomini e delle donne verticalmente, si nasconde la maggior redditività. Lo stiramento della scala orizzontale aiuta anche a nascondere quelsiasi tendenza futura.
la strada dell'inferno è pavimentata con...
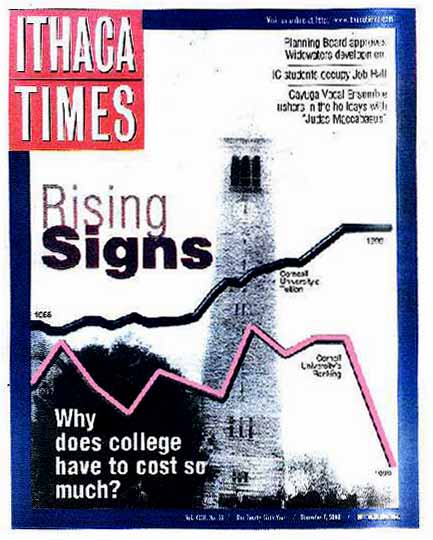 Questa immagine, tratta dalla copertina dell rivista Ithaca Times (7 dic. 2000) può ben essere il grafico più ingannevole mai pubblicato. Esso propone un esempio spettacolare di manipolazione grafica.
Questa immagine, tratta dalla copertina dell rivista Ithaca Times (7 dic. 2000) può ben essere il grafico più ingannevole mai pubblicato. Esso propone un esempio spettacolare di manipolazione grafica.
La copertina, che riporta il titolo: "Perché i college devono costare così tanto?" mostra un ampio grafico sovraimpresso ad un'immagine del campus Cornell. Ci sono due linee seghettate che salgono lungo il grafico, una etichettata "Costi della Cornell" e l'altra "Livello della Cornell". Il grafico dei costi mostra un aumento costante ed il grafico del livello, dopo alcuni serpeggiamenti precipita verso il basso. L'impressione evidente è che gli studenti stanno pagando di più per meno.
Nel prossimo punto viene discussa la costruzione di questa bugia.
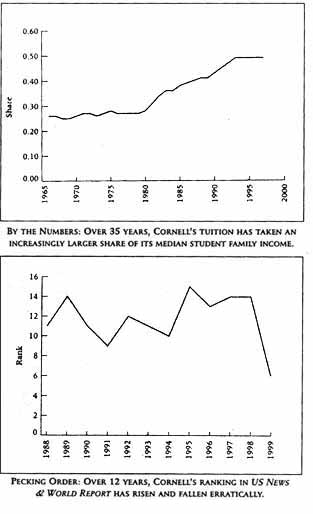 Cosa hanno di sbagliato questi due grafici?
Cosa hanno di sbagliato questi due grafici?
Un'attenta lettura dell'intero articolo precedente rivela cose differenti:
1) il grafico della classificazione copre un periodo di 11 anni, il grafico delle tasse scolastiche si riferisce a 35 anni, tuttavia questi grafici sono mostrati simultaneamente (con la stessa larghezza apparente) sullo stesso asse orizzontale;
2) la scala verticale per livello e tasse potrebbe non avere unità comuni, ma il grafico del livello è collocato sopra il grafico delle spese creando l'impressione che i costi superino la qualità;
3) le differenti unità di tempo sono abilmente mascherate stampandole ruotate di 900;
4) ed ecco il colpaccio: la brusca caduta nel grafico del livello degli anni passati in realtà rappresenta il fatto che il livello della Cornell è migliorato dal 15o al 6o posto!
Alcuni esempi discussi sono stati tratti dal sito: www.math.yorku.ca/SCS/Gallery/noframes.html#Goosed
Marcello Guidotti, copyright 2003-2006-2010 - ultimo aggiornamento 13 settembre 2010
questa pagina può essere riprodotta su qualsiasi supporto o rivista purché sia citata la fonte e l'indirizzo di questo sito (ai sensi degli artt. 2575 e 2576 cc. Legislazione sul diritto d'autore). Le fotografie sono tratte da siti web e sono, o possono ritenersi, di pubblico dominio purché utilizzate senza fini di lucro. Le immagini di prodotti presenti nel sito hanno unicamente valenza esemplificativa oltre che, eventualmente, illustrare messaggi fuorvianti e non vi è alcun richiamo diretto o indiretto alla loro qualità e/o efficacia il cui controllo è affidato alle autorità regolamentatorie.
 Con il termine anglosassone spin doctor, si indica una persona esperta nel cosigliare altre persone (politici, manager, economisti, opinionisti) su come distorcere la verità, o se si preferisce, individuare all'interno di una raccolta di dati oggettivi un modo per renderli soggettivi... cioè presentarli secondo un certo punto di vista.
Con il termine anglosassone spin doctor, si indica una persona esperta nel cosigliare altre persone (politici, manager, economisti, opinionisti) su come distorcere la verità, o se si preferisce, individuare all'interno di una raccolta di dati oggettivi un modo per renderli soggettivi... cioè presentarli secondo un certo punto di vista.

 Il direttore marketing di un'azienda farmaceutica, riferendo un comunicato aziendale, coglie l'occasione per uno sprone:
Il direttore marketing di un'azienda farmaceutica, riferendo un comunicato aziendale, coglie l'occasione per uno sprone:

 Un altro elemento chiave nel produrre grafici informativi è evitare di confondere le variazioni negli elementi del disegno con le variazioni dei dati. Ciò comporta che i cambiamenti nella scala dei grafici dovrebbero sempre corrispondere ai cambiamenti dei dati da rappresentare. Questo grafico vìola questo principio usando le dimensioni dei medici per mostrare dati mono-dimensionali, dando un fattore di inganno (2.8) più contenuto rispetto al caso precedente.
Un altro elemento chiave nel produrre grafici informativi è evitare di confondere le variazioni negli elementi del disegno con le variazioni dei dati. Ciò comporta che i cambiamenti nella scala dei grafici dovrebbero sempre corrispondere ai cambiamenti dei dati da rappresentare. Questo grafico vìola questo principio usando le dimensioni dei medici per mostrare dati mono-dimensionali, dando un fattore di inganno (2.8) più contenuto rispetto al caso precedente.
 Una variante del fattore di scala è si ottiene modificando la scala delle ordinate in modo da ottenere una pendenza differente. I due istogrammi riportano i fatturati e quindi la penetrazione commerciale delle aziende XXX e YYY. Scegliendo opportunamente la scala delle ordinate, si può suggerire che l'azienda YYY abbia un incremento di fatturato maggiore.
Una variante del fattore di scala è si ottiene modificando la scala delle ordinate in modo da ottenere una pendenza differente. I due istogrammi riportano i fatturati e quindi la penetrazione commerciale delle aziende XXX e YYY. Scegliendo opportunamente la scala delle ordinate, si può suggerire che l'azienda YYY abbia un incremento di fatturato maggiore.


 Questo grafico, proveniente da Social Indicators III, si propone di confrontare le tendenze nei redditi mediani di uomini e donne per livello d'istruzione. Ma impilando i grafici degli uomini e delle donne verticalmente, si nasconde la maggior redditività. Lo stiramento della scala orizzontale aiuta anche a nascondere quelsiasi tendenza futura.
Questo grafico, proveniente da Social Indicators III, si propone di confrontare le tendenze nei redditi mediani di uomini e donne per livello d'istruzione. Ma impilando i grafici degli uomini e delle donne verticalmente, si nasconde la maggior redditività. Lo stiramento della scala orizzontale aiuta anche a nascondere quelsiasi tendenza futura.
 Questa immagine, tratta dalla copertina dell rivista Ithaca Times (7 dic. 2000) può ben essere il grafico più ingannevole mai pubblicato. Esso propone un esempio spettacolare di manipolazione grafica.
Questa immagine, tratta dalla copertina dell rivista Ithaca Times (7 dic. 2000) può ben essere il grafico più ingannevole mai pubblicato. Esso propone un esempio spettacolare di manipolazione grafica.
 Cosa hanno di sbagliato questi due grafici?
Cosa hanno di sbagliato questi due grafici?