test di significatività

Affidandoci al senso comune, tendiamo senz'altro a rispondere affermativamente. D'altra parte, l'epidemiologo, di fronte ad una domanda dei questo tipo, ritiene sia più corretta una risposta del tipo «non è possibile rispondere in quanto i dati forniti sono insufficienti».

Nella statistica, infatti, il termine "associazione" assume un significato diverso da quello comune; infatti, nel linguaggio parlato due eventi si dicono associati quando compaiono o si verificano solitamente in correlazione l'uno con l'altro... per la statistica, due eventi si dicono "associati" solo quando sono correlati in modo maggiore di quanto si verifichi per puro caso.

il test del chi-quadro

Tutti i metodi che si basano su distribuzioni probabilistiche dei dati, quali la distribuzione normale, sono detti parametrici. In contrapposizione, le tecniche non parametriche sono quelle che non sono basate su alcuna distribuzione probabilistica. In generale i test non parametrici dovrebbero essere preferiti quando i dati non si distribuiscono secondo una normale, o comunque non si è in grado di dimostrarlo, ad esempio per numerosità ridotta.
Il test del chi-quadro è un test statistico non parametrico atto a verificare se i valori di frequenza ottenuti tramite rilevazione, sono diversi in maniera significativa dalle frequenze ottenute con la distribuzione teorica. Questo test ci permette di accettare o rifiutare una data ipotesi.

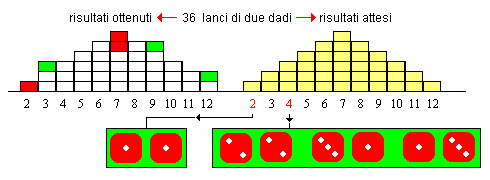
L'istogramma sopra a sinistra, mostra i risultati ottenuti dal lancio di due dadi ripetuto per 36 volte. A destra, sono riportati i risultati attesi (dopo 36 lanci) in base alla probabilità di uscita dei vari risultati : ottenere un 2 con due dadi è più difficile che ottenere un 4 (con 4 lanci ci si può aspettare che esca un 2 e tre volte 4). Ancóra, nell'istogramma a sinistra, le differenze positive (risultati oltre il previsto) sono rappresentate da zone colorate in verde; quelle negative, da zone colorate in rosso. Supponendo che dopo un certo numero di lanci, si ottenga una serie di lanci "non fortunati", diremo che la "sfortuna" ci perseguita se l'istogramma di sinistra si discosta oltre un certo valore da quella che sarebbe la distibuzione dei risultati attesi. Diversamente, diremo che le nostre perdite sono una semplice conseguenza del caso (qualche volta si vince e qualche volta si perde, anche se generalmente tendiamo a prestare maggior attenzione alle perdite).

Il test con il quale si decide se due o più eventi sono tra loro associati, oppure una semplice conseguenza della probabilità, utilizza la cosiddetta ipotesi zero, Ho.

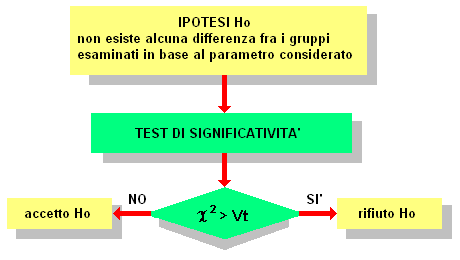
Il diagramma in alto illustra i passi per effettuare un test di significatività:

1. formulazione dell'ipotesi Ho: gli eventi osservati sono dovuti al caso; non esiste alcuna correlazione tra loro;
2. per verificare l'ipotesi Ho applichiamo il test, che può risultare:
   • positivo: accettiamo l'ipotesi Ho tra gli eventi osservati non esiste una correlazione
   • negativo: rifiutiamo l'ipotesi Ho tra gli eventi osservati esiste una correlazione

gradi di libertà probabilità 10% 5% 1% 1 2.71 3.84 6.63 2 4.61 5.99 9.21 3 6.25 7.81 11.34 4 7.78 9.49 13.28 5 9.24 11.07 15.00

Per eseguire il test, occorre calcolare e confrontarlo con Vt. Esaminando la formula per calcolare (incorniciata in verde), si nota che contiene una somma di termini (numeri osservati e numeri attesi) elevati al quadrato in modo da restituire comunque un numero positivo (nell'istogramma relativo al lancio dei dadi, le zone in rosso e le zone in verde non devono compensarsi reciprocamente); inoltre, è evidente che maggiore è la differenza fra valori osservati e valori attesi, maggiore sarà il risultato. Quanto più alto è questo risultato, tanto maggiore è la probabilità che la relazione non sia causale.

Per ottenere Vt, si utilizzano i dati riportati in tabella (v. esempi seguenti) rispettando due criteri:

1. il numero di gradi di libertà, che in una tabella formata da r righe e c colonne, è dato da: (r - 1) x (c - 1);
2. il valore massimo per il quale, in corrispondenza di una certa probabilità e dei gradi di libertà del sistema in studio, dobbiamo accettare l'ipotesi Ho. Se questo valore è superato, allora rifiutiamo Ho.

• l'ipotesi zero è respinta per 4,61 (10%) : con probabilità del 90% i dati ottenuti non sono dovuti al caso (esiste però la probabilità del 10% che i dati siano casuali);
• l'ipotesi zero è respinta per 5,99 (5%) : con probabilità del 95% i dati ottenuti non sono dovuti al caso (esiste però la probabilità del 10% che i dati siano casuali);
• l'ipotesi zero è accettata per 9,21 (1%) : con probabilità del 99% i dati ottenuti sono dovuti al caso (esiste però la probabilità del 1% che i dati non siano casuali).

Gli esempi applicativi che seguono mostrano come l'applicazione del test non presenti difficoltà. Però, occorre tenere a mente che qualsiasi risultato è sempre associato ad una probabilità. Questo significa che se l'ipotesi H0 è accettata, la distribuzione dei dati controllata è dovuta al caso (ma non lo è con una certa probabilità); se è rifiutata, la distribuzione dei dati non è dovuta al caso (ma lo è con una certa probabilità). Queste precisazioni sono necessarie in quanto se fosse possibile ottenere una probabilità del 100%, il procedimento induttivo avrebbe la stessa efficacia epistemologica di quello deduttivo. E questo è impossibile per definizione (v. riquadro).

E' noto che la conoscenza si sviluppa attraverso due procedimenti: deduttivo e induttivo. Il primo, parte da un certo assunto e da questo si deduce una conclusione. Per esempio, poiché la somma degli angoli interni ad un quadrato è 360º, la somma degli angoli interni ai singoli due triangoli rettangoli in cui può essere scomposto è 180º. Il metodo induttivo, si sviluppa in modo opposto: per esempio, dall'esame di un certo numero di conigli, si conclude che sono vegetariani, però questa è una inferenza speculativa in quanto non sono stati osservati "tutti" i conigli e, per quanto siano molti non sono "tutti". Dunque, con il metodo induttivo, si può inferire che tutti i conigli esaminati mangiano verdura e per gli altri probabilmente è così!

esempi applicativi

esempio 2: si vuole verificare quale di due farmaci è più efficace. A questo scopo, 23 pazienti vengono trattati con il farmaco A e 17 con il farmaco B. Dei 23 pazienti trattati con A, 13 risultano guariti, mentre dei 17 trattati con B ne risultano guariti 8. terapia diagnosi Totale guariti non guariti A 13 10 23 B   8   9 17 totale parziale 21 19 40 La percentuale di guarigione per entrambe i due trattamenti è complessivamente 21/40 = 0,525 = 52,5% Con questa percentuale, costruiamo la tabella dei valori attesi: terapia diagnosi Totale guariti non guariti A 12 11 23 B   9   8 17 totale parziale 21 19 40 il calcolo del fornisce: = (13 - 12)2/12 + (10 - 11)2/11 + (8 - 9)2/9 + (9 - 8)2/8 = 0,41 Dall'esame della tabella risulta che il valore 0,41 con 1 grado di libertà, è minore di 2.71 (P = 10%) e dunque dobbiamo accettare l'ipotesi Ho. Questo significa che non vi sono margini statistici per stabilire se il farmaco A è più efficace della terapia B. Detto diversamente, la differenza nelle guarigioni ottenute tra la terapia con A (10/23 = 56%) e con B (8/17 = 47%) ha il 90% di probabilità di essere dovuta al caso.

esempio 3: in un campione di N = 70 unità statistiche vengono rilevati due caratteri X (reddito) ed Y (rendimento scolastico); raggruppando i valori osservati di X in 3 classi, e quelli di Y anche in 3 classi, si ottiene la seguente tabella di contingenza: reddito (X) rendimento (Y) Totale buono discreto scarso basso 7 5 7 19 medio 12 7 6 25 alto 15 8 3 26 Totale parziale 34 20 16 70 le percentuali sui totali parziali sono rispettivamente: prima colonna: 34/70 = 0.5 seconda colonna: 20/70 = 0.3 terza colonna: 16/70 = 0,2 con questi valori generiamo la tabella dei risultati attesi: reddito (X) rendimento (Y) Totale buono discreto scarso basso 9,12 5,72 4,16 19 medio 12,40 7 5,60 25 alto 12,48 7,28 6,24 26 Totale parziale 34 20 16 70 il calcolo del fornisce: = (7 - 9,12)2/9,12 + (12 - 12,40)2/12,40 + (15 - 12,48)2/12,48 + (5 - 5,72)2/5,72 + (7 - 7)2/7 + (8 - 7,28)2/7,28 + (15 - 12,48)2/12,48 + (8-7,28)2/7,28 + (3 - 6,24)2/6,24 = 3,35 Dall'esame della tabella risulta che il valore 3,35 con (3-1)x(3-1) = 4 gradi di libertà, è minore di 7.78 (P = 10%) e dunque dobbiamo accettare l'ipotesi Ho. Questo significa che non vi sono margini statistici per stabilire se c'è correlazione fra reddito ed rendimento scolastico. Detto diversamente, la differenza (per il campione ipotizzato) è verosimilmente dovuta al caso. In alcuni casi, è possibile che un confronto "due a due" dia un risultato differente, cioè evidenzi una correlazione. Così, prima di gettare al vento i dati raccolti, potrebbe essere interessante comporre nuove tabelle in modo da proporre, con gli stessi dati, confronti differenti (per es., reddito alto e reddito basso). esempio 4: in un'indagine epidemiologica si sono campionate 100 persone secondo i seguenti caratteri: A = influenzato durante l'inverno, B = generalmente usa i mezzi pubblici, ottenendo la seguente tabella: utente influenzato non influenzato totali usa mezzi pubblici 50 16 66 non usa mezzi pubblici 12 22 34 totali parziali 62 38 100 Dopo aver costruito la tabella dei risultati attesi, il lettore può verificare che il valore di è 15.59. I gradi di libertà sono (2-1)x (2-1) =1. Dalla tabelle risulta che il valore trovato è maggiore di 6.63 (P 1%). Concludiamo (per questo caso ipotetico) che ci sia una probabilità del 99% a favore delle correlazione fra l'uso dei mezzi pubblici e la probabilità di contrarre l'influenza.

correzione di Yates

Il procedimento di calcolo comporta la sottrazione di 0,5 alla differenza fra valori osservati e valori attesi:

test esatto di Fisher

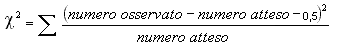
	gruppo 1 (farmaco A)	gruppo 2 (farmaco B)
guariti	3	6	9
non guariti	4	2	6
	7	8	15

Come primo passo, si riarrangia la tabella in modo da azzerare il valore della cella che contiene il valore più basso (nel caso in esame è n_2,2 = 2). Per conseguenza i valori delle altre celle cambieranno in modo da mantenere costanti i totali parziali.

	gruppo 1 (farmaco A)	gruppo 2 (farmaco B)
guariti	1	8	9
non guariti	6	0	6
	7	8	15

a questo punto si applica alle due tabelle la formula dimostrata da Fisher :

In pratica, le lettere a, b, c, d, corrispondono al contenuto delle celle, n alla numerosità del campione e col simbolo ! si intende l'operatore fattoriale (3! = 3 · 2 · 1 = 6 ; 2! = 2 · 1 = 2 ; 1! = 1 ; 0! = 1).

prima tabella P1 = (3 + 6)! (4 + 2)! (3 + 4)! (6 + 2)! /(15! 3! 6! 4! 2!) = 0,195

seconda tabella P2 = (1 + 8)! (6 + 0)! (1 + 6)! (8 + 0)!/15! 1! 8! 6! 0!) = 0,001

sommando le due probabilità si ottiene P = 0,196 % questo significa che se l'ipotesi nulla è vera (cioè i due trattamenti sono equivalenti), allora solo in allora 19 casi su 10.000 si otterrebbero valori così discordanti tra in due gruppi.

Questo calcolo, come per quello del "chi-quadro" è molto laborioso, per questo si ricorre solitamente al calcolatore usando software applicativi per la statistica.

osservazioni da non sottovalutare

Il paradosso di Simpson, ricordato nella statistica descrittiva, fornisce un buon esempio per comprendere l'ultilità di un test di inferenza statistica.

Nell'esempio ricordato, abbiamo visto che due studi indipendenti per provare l'efficacia di un farmaco A rispetto ad un farmaco B hanno dato i risultati riassunti nelle due tabelle che seguono.

Ora, calcoliamo le percentuali di guariti riportate dal primo studio: farmaco A = 60/75 = 0,8 ; farmaco B = 45/65 = 0,69

le percentuali di guariti riportate dal secondo studio danno: farmaco A = 95/185 = 0,51 ; farmaco B = 5/15 = 0,33

E' ovvio concludere che il farmaco A è più efficace del farmaco B. Ovvio?
Ora, calcoliamo le percentuali dei guariti con il farmaco A sommando i risultati dei due studi: (60 + 95)/(75 + 185)= 0,60
calcoliamo le percentuali dei guariti con il farmaco B sommando i risultati dei due studi: (45 + 5)/(65 + 15) = 0,62
Il farmaco B è più efficace del farmaco A, o comunque la differenza di efficacia sembra irrilevante.

guariti non guariti farmaco A (totale) 155 105 260 farmaco B (totale) 50 30 80 205 135 340

Questo risultato paradossale, trova una spiegazione nel fatto che aggregando dati ottenuti da sperimentazioni diverse non si considerano elementi che, se esplicitati, avrebbero evidenziato differenze tra i due campionamenti (per es. differente percentuale di uomini e donne, differenze di peso, ecc.). In questo caso, il test del Chi-quadro applicato alle tre tabelle, mostra come l'ipotesi nulla sia sempre accettata: non esistono differenze statisticamente significative per concludere la maggior efficacia di uno dei due farmaci e dunque, l'inferenza che conduce al paradosso non è corretta.

Si deve sempre tener presente che qualsiasi test che permetta di stabilire la fiducia accordata nel rifiutare l'ipotesi nulla, non implica necessariamente una relazione di causa-effetto tra le variabili esaminate. Questo assunto, che avvaloreremo con gli esempi che seguono, rende ragione del fatto che solo i processi deduttivi portano a inferenze certe, mentre questo non è possibile per i processi induttivi. D'altra parte, mentre nei processi deduttivi le inferenze sono già implicite nelle premesse (si tratta di evidenziarle), questo non è vero per i processi induttivi (la cui generalizzazione costituisce comunque un salto nel buio).

Frederick Mosteller (1916 - 2006), lavorando presso il Samuel Wilks's Statistical Research Group durante la II Guerra Mondiale, esaminò alcune questioni statistiche a proposito di associazione non causale. Nel corso della guerra, si era riscontrato un fatto paradossale: i bombardamenti alleati in Europa risultavano tanto più precisi quanto maggiore era il numero di caccia nemici decollati per intercettarli e quanto più intensa era la reazione della contraerea. Però, questa curiosa correlazione era apparente... Infatti, in condizioni di cielo nuvoloso, le nuvole impedivano ai bombardieri la visibilità degli obiettivi; per la stessa ragione, la contraerea e l'azione dei caccia si dimostrava scarsamente efficace. Viceversa, in condizioni di cielo sereno, la visibilità degli obiettivi era ottimale ma la contraerea ed i caccia offrivano una forte difesa.
In conclusione, l'apparente associazione di causalità (bombardamenti più efficaci quanto più intensa era l'azione della contrarerea e più elevato il numero di caccia) era mediata dal fattore "nuvole".

Come altro esempio, possiamo citare una vecchia indagine svolta in Usa, su un campione di donne: si evidenziò una forte correlazione positiva tra l'avere il cancro ai polmoni e il portare le calze di seta.
Poiché certamente il cancro ai polmoni non induceva le donne a portare le calze di seta, potrebbe sembrare vero il contrario... In realtà, le calze di seta erano abbinate ad un comportamento sociale che imponeva anche la sigaretta e dunque la correlazione cancro ai polmoni-sigaretta era mediata da un fattore, le calze di seta, estraneo alla relazione di causalità.

Sulla scorta di questo esempi, in termini più generali, si può concludere che in presenza di un'associazione causale tra A e B, può verificarsi che in realtà entrambi dipendano da un terzo fattore X.
Per esempio, un campione studiato con bassa validità interna, può portare a correlazioni affette da bias.

1	2	3	4	5	6	7
HOME PAGE

Marcello Guidotti, copyright 2003, 2005, 2007, 2010, 2011
questa pagina può essere riprodotta su qualsiasi supporto o rivista purché sia citata la fonte e l'indirizzo di questo sito (ai sensi degli artt. 2575 e 2576 cc. Legislazione sul diritto d'autore). Le fotografie sono tratte da siti web e sono, o possono ritenersi, di pubblico dominio purché utilizzate senza fini di lucro. Le immagini di prodotti presenti nel sito hanno unicamente valenza esemplificativa oltre che, eventualmente, illustrare messaggi fuorvianti e non vi è alcun richiamo diretto o indiretto alla loro qualità e/o efficacia il cui controllo è affidato alle autorità regolamentatorie.