| prescrizioni | max | min | media |
| medici zona A | 190 | 60 | 100 |
| medici zona B | 310 | 70 | 80 |
A parità di altre condizioni, quanto più alta è la variabilità di un fenomeno rilevata con gli indici di dispersione, tanto meno significativo è l'uso della media aritmetica per definire sinteticamente una distribuzione.
nel caso la serie di valori rilevata non sia tale da costituire l'inviluppo di una Gaussiana, cosa che accade per le misurazioni che comunemente riguardano le sperimentazioni cliniche, allora i suddetti limiti sono da ritenersi un'indicazione del numero massimo di dati che cadono all'interno di ogni intervallo. Per es, su dieci dati, nel primo intervallo possono caderne solo quattro, piuttosto che sei.
|
esempio: per rendere più evidente il paradosso statistico del "pollo di Trilussa", immaginiamo, senza stravolgerne il senso, che le osservazioni sul numero di polli consumati si riferiscano all'arco di due giorni, e siano [0, 2], cioè nessun pollo il primo giorno e due polli il secondo giorno.
Poiché la deviazione standard si allontana dalla media solo per l'estremo positivo ( |
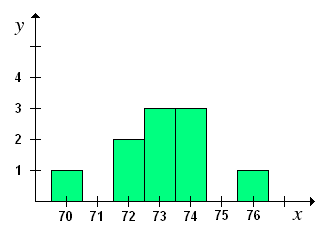
I dati sono presentati nel formato [a1, a2, a3, ... an] e la loro rappresentazione grafica è ottenuta portando in ascisse le coordinate alle quali corrispondono le singole osservazioni, an, ed in ordinate la frequenza con cui compaiono le osservazioni. Per esempio, [73, 72, 73, 74, 70, 76, 72, 74, 74, 73] sono dati che si riferiscono al numero di battiti cardiaci al minuto registrati nell'arco di 10 giorni ad un paziente. Allora, in ascisse riporteremo i battiti registrati, ed in ordinate la frequenza con cui compaiono (tre volte 73, due volte 72, ecc.). In questo modo, si ottiene il grafico discusso alla pagina precedente.
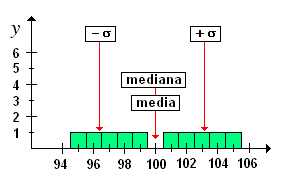 esempio 1: studiare la curva di distribuzione i cui valori sono:
95, 96, 97, 98, 99, 101, 102, 103, 104, 105 esempio 1: studiare la curva di distribuzione i cui valori sono:
95, 96, 97, 98, 99, 101, 102, 103, 104, 105
il campo di variazione è: 105 - 95 = 10 la media è: 100 e non corrisponde ad alcun valore realmente osservato; la mediana è: 100 ed è uguale alla media; ciò indica una distribuzione simmetrica la moda è mancante la deviazione standard è: 3.3 ed indica che la media fornisce una stima adeguata delle misure osservate. Infatti, nell'intervallo (100 - 3.3); (100 + 3.3) cadono 6 valori su 10 il coefficiente di variazione è: 3,3/ 100 = 0.033, un valore molto basso e quindi la media è un indicatore corretto. |
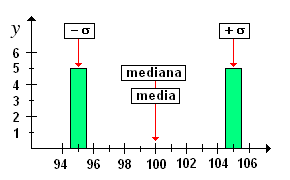 esempio 2: studiare la curva di distribuzione i cui valori sono: 95, 95, 95, 95, 95, 105, 105, 105, 105, 105 esempio 2: studiare la curva di distribuzione i cui valori sono: 95, 95, 95, 95, 95, 105, 105, 105, 105, 105
il campo di variazione è: 105 - 95 = 10 la media è: 100 e non corrisponde ad alcun valore realmente osservato; la mediana è: 100 ed è uguale alla media; ciò indica una distribuzione simmetrica la moda è: bimodale, con i valori 95 e 100. Questo è l'indicatore più appropriato per la distribuzione in oggetto. la deviazione standard è: 5 ed indica che la media fornisce una stima adeguata delle misure osservate. Infatti, nell'intervallo (100 - 5); (100 + 5) cadono 10 valori su 10
il coefficiente di variazione è: 5/ 100 = 0.05, un valore basso. Inoltre, poiché l'intervallo (s ± |
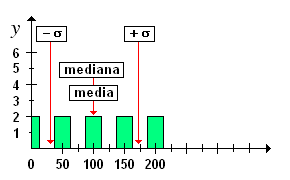 esempio 3: studiare la curva di distribuzione i cui valori sono: 0, 0, 50, 50, 100, 100, 150, 150, 200, 200 esempio 3: studiare la curva di distribuzione i cui valori sono: 0, 0, 50, 50, 100, 100, 150, 150, 200, 200
il campo di variazione è: 200 - 0 = 200 la media è: 100 corrisponde a due valori realmente osservati; la mediana è: 100 ed è uguale alla media; ciò indica una distribuzione simmetrica la moda è: plurimodale la deviazione standard è: 70,7 ed indica che la media fornisce una stima adeguata delle misure osservate. Nell'intervallo (100 - 70,7); (100 + 70,7) cadono 6 valori su 10 e l'intervallo in cui cadono i dati è coperto al 50% il coefficiente di variazione è: 70.7/ 100 = 0.7 un valore alto, e quindi l'indicatore più adatto è la moda in quanto la distribuzione è multimodale. |
|
esempio 4: studiare la curva di distribuzione i cui valori sono: 20, 40, 50, 60, 70, 80, 90, 90, 100, 200, 200, 200
il campo di variazione è: 200 - 20 = 180 la media è: 100 e corrisponde ad un valore realmente osservato; la mediana è: 85 ed è differente dalla media; ciò indica una distribuzione asimmetrica
la deviazione standard è: 61.6 e la media fornisce una stima adeguata delle misure osservate. il coefficiente di variazione è: 61.6/ 100 = 0.62 un valore elevato, infatti i valori osservati sono piuttosto distribuiti.
La presenza di un valore estremo (200) provoca una distorsione sugli indici di variabilità e toglie significato rappresentativo alla media. Questo è un caso piuttosto frequente in campo medico (per es., i valori degli esami del sangue) ed in altri settori applicativi. |
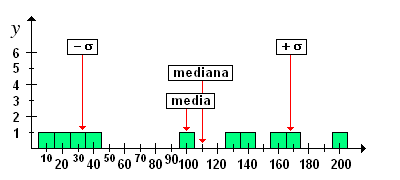 esempio 5: studiare la curva di distribuzione i cui valori sono: 10, 20, 30, 40, 100, 130, 140, 160, 170, 200 esempio 5: studiare la curva di distribuzione i cui valori sono: 10, 20, 30, 40, 100, 130, 140, 160, 170, 200
il campo di variazione è: 200 - 10 = 190 la media è: 100 e corrisponde ad un valore realmente osservato; la mediana è: 115 ed è differente dalla media; ciò indica una distribuzione asimmetrica la moda è mancante. la deviazione standard è: 66.3 ed indica che la media non fornisce una stima adeguata delle misure osservate, infatti, in questo caso, 5 valori su 10 rientrano nell'intervallo (100 - 66.3) e (100 + 66.3) il coefficiente di variazione è:69.9/ 100 = 0.69 un valore molto elevato, infatti la distribuzione dei dati è estesa. |
| 3 | |||
Marcello Guidotti, copyright 2003
questa pagina può essere riprodotta su qualsiasi supporto o rivista purché sia citata la fonte e l'indirizzo di questo sito (ai sensi degli artt. 2575 e 2576 cc. Legislazione sul diritto d'autore). Le fotografie sono tratte da siti web e costituiscono materiale pubblicitario, oppure sono, o possono ritenersi, di pubblico dominio purché utilizzate senza fini di lucro.