statistica descrittiva

1. statistica descrittiva: il suo obiettivo è ricavare da un insieme di dati raccolti in tabelle e grafici (troppo numerosi per poter essere esaminati singolarmente) alcune informazioni significative per il problema studiato;
2. statistica inferenziale: il suo obiettivo è fornire metodi che servono ad imparare dall'esperienza, cioè a costruire modelli per passare da casi particolari al caso generale. Nella statistica inferenziale o induttiva, si usano anche tecniche del calcolo delle probabilità.

media, moda e mediana

• media: è la somma di tutte le N osservazioni divisa per N. Per es., per i valori [1, 2, 4, 4, 5, 7, 9, 11], la media è 43/8

• moda: è il numero di osservazioni che compare con maggior frequenza. Per es., per i valori [1, 2, 4, 4, 5, 7, 9, 11], la moda è 4. In alcune distribuzioni, la moda può mancare, oppure essere presente per più di un valore; in questo caso, si hanno distribuzioni bimodali (due mode), trimodali (tre mode), plurimoldali

• mediana: è il numero cche compare al centro dei valori osservati, se questi sono dispari; se sono pari, è la media fra i due valori centrali. Per es., per i valori [1, 2, 4, 4, 5, 7, 9, 11], la mediana è (4 + 5)/2

Effettivamente, se abbiamo due misurazioni, [0, 2], per esempio riferite proprio a due persone, una sola delle quali mangia due polli, la media fornisce il valore 1, e quindi risulta un pollo a testa
Questa situazione "imbarazzante", però è superabile mediante la stima fornita dalla deviazione standard e degli indicatori statistici che esamineremo nella prossima pagina.

deviazione standard

Per dare una valutazione dell'incertezza da associare a tale stima, iniziamo col considerare una prima quantità chiamata scarto o deviazione. Tale grandezza è così definita:

d = x -

Questa differenza fornisce una indicazione di quanto una qualsiasi misura differisce dalla media. In generale, se tutti gli scarti sono molto piccoli, le nostre misure saranno tutte vicine e quindi, presumibilmente, molto precise.
Oltre al valore numerico degli scarti, indice di precisione nelle misure, è interessante notarne il segno: le deviazioni possono essere infatti sia positive che negative a seconda che una qualsiasi delle N misure cada a destra o a sinistra della media.

Questo fatto complica un pò la situazione. Infatti, se volessimo provare a valutare l'incertezza attraverso una media dei singoli scarti, ci accorgeremmo subito che la media degli scarti è uguale a zero.

Possiamo rapidamente verificare questo fatto nel caso semplice di due misure: x1, x2; la loro media è : = (x1 + x2)/2 I singoli scarti sono: d1 = x1 - ;   d2 = x2 - la somma degli scarti é: d1 + d2 = (x1 - ) + (x2 - ) reggruppando: d1 + d2 = (x1 + x2) - 2. Essendo nullo il secondo membro, risulta d1 + d2 = 0

Non dovremmo però rimanere sorpresi per questo risultato valido in generale: la media, per definizione, è tale per cui i dati si distribuiscono sia alla sua sinistra che alla sua destra, facendo sì che la somma tra gli scarti negativi e quelli positivi sia appunto nulla.

Poiché gli scarti costituiscano un buon punto di partenza per lo studio dell'incertezza da associare alla media, per ovviare all'inconveniente legato alla loro somma, eleviamo al quadrato le singole deviazioni ottenendo tutte quantità positive e quindi in grado di essere sommate tra loro senza produrre in un risultato nullo.
Dopodiché si può passare a calcolare la media degli scarti estraendone la radice quadrata, in modo da ottenere una grandezza compatibile, a livello di unità di misura, con quella di partenza. La grandezza così ottenuta è detta deviazione standard.

(1)     (2)

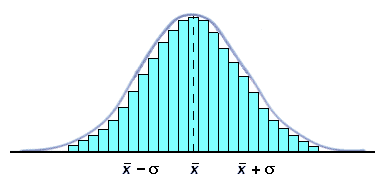Approssimazione di una Gaussiana mediante un istogramma

Quando i dati sperimentali sono molti, raccogliendoli in un istogramma (diagramma a barre), viene approssimano per difetto il profilo di una curva detta Gaussiana, dal nome del matematico Carl F. Gauss (1777-1855). Per una Gaussiana, è possibile dimostrare che nell'intervallo:

• ( - s < < + s) cade il 68.7% delle misure rilevate;
• ( - 2 s < < + 2 s) cade il 95.45% delle misure rilevate;
• ( - 3 s < < + 3 s) cade il 99.73% delle misure rilevate.

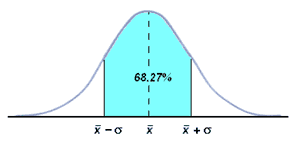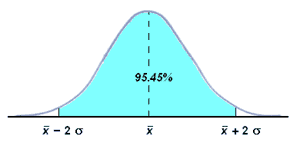esempio: Disegnare l'istogramma delle frequenze (v. fig. a destra) e calcolare le stime campionarie per un paziente del quale è stati registrato il seguente numero di battiti cardiaci al minuto in un periodo di 10 giorni: [73, 72, 73, 74, 70, 76, 72, 74, 74, 73] Le stime campionarie sono: la media è: Sosservazioni/N = (73 + 72 + 73 + 74 + 70 + 76 + 72 + 74 + 74 + 73)/10 = 73,1 la mediana, trattandosi di un insieme costituito da osservazioni in numero pari, è data dalla media dei valori centrali: 70, 72, 72, 73, 73, 73, 74, 74, 74, 76 (73 + 73)/2 = 73 la moda è bimodale, ed è costituita dai due valori più frequenti: 73 e 74 la deviazione standard (eq. 2) è: s = 1.59 questo significa che il 68% delle misure deve rientrare nell'intervallo (73,1 - 1,59) e (73,1 + 1,59), cioè tra + 71,5 e + 74,7. Le misure che cadono in questo intervallo sono: 72, 72, 73, 73, 73, 74, 74, 74; cioé 7 su 10.

1	2	3	4
HOME PAGE

Marcello Guidotti, copyright 2003
questa pagina può essere riprodotta su qualsiasi supporto o rivista purché sia citata la fonte e l'indirizzo di questo sito (ai sensi degli artt. 2575 e 2576 cc. Legislazione sul diritto d'autore). Le fotografie sono tratte da siti web e sono, o possono ritenersi, di pubblico dominio purché utilizzate senza fini di lucro. Le immagini di prodotti presenti nel sito hanno unicamente valenza esemplificativa oltre che, eventualmente, illustrare messaggi fuorvianti e non vi è alcun richiamo diretto o indiretto alla loro qualità e/o efficacia il cui controllo è affidato alle autorità regolamentatorie.